Feladat:	B.4284	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Strenner Péter
Füzet:	2011/május, 281 - 282. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Síkgeometriai bizonyítások, Érintőnégyszögek, Trapézok, Középpontos tükrözés
Hivatkozás(ok):	Feladatok: 2010/szeptember: B.4284

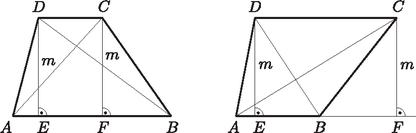
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Megoldás. Az $ABCD$ érintőtrapéz alapjai legyenek $AB$ és $CD$, magassága $m$. A $C$ és $D$ csúcsok $AB$ egyenesen lévő merőleges vetületeit jelölje $F$ és $E$. Tegyük fel, hogy mindkét átló ${45}^{\circ }$-nál nagyobb szöget zár be az alapokkal. Ekkor az $AFC$ és $BED$ derékszögű háromszögekben $FC$ és $ED$ a hosszabb befogók, tehát $\begin{array}{c}{\displaystyle AF+BE<FC+ED=2m\le BC+DA\mathrm{.}}\end{array}$ (1) Megmutatjuk, hogy $AF+BE=AB+CD$. Az $A$, $B$, $E$, $F$ pontok sorrendje többféle lehet (lásd az ábrákat), ezért a diszkussziót elkerülendő, vektorok segítségével bizonyítunk. Nyilván igaz, hogy $\begin{array}{c}{\displaystyle \overrightarrow{AF}+\overrightarrow{FC}+\overrightarrow{CD}+\overrightarrow{DE}+\overrightarrow{EB}+\overrightarrow{BA}=\text{0}\mathrm{.}}\end{array}$ Mivel $\overrightarrow{FC}=-\overrightarrow{DE}$, ebből átrendezéssel kapjuk, hogy $\begin{array}{c}{\displaystyle \overrightarrow{AF}+\overrightarrow{EB}=-\overrightarrow{CD}-\overrightarrow{BA}=\overrightarrow{DC}+\overrightarrow{AB}\mathrm{.}}\end{array}$ Mivel ezek a vektorok mind párhuzamosak a trapéz alapjaival, azért egyenlőségük a megfelelő szakaszok hosszának egyenlőségét is jelenti, tehát $AF+BE=AB+CD$. Ezt az (1) egyenlőségbe beírva kapjuk, hogy $\begin{array}{c}{\displaystyle AB+CD=AF+BE<BC+DA\mathrm{.}}\end{array}$ Ez viszont ellentmondás, mert bármely érintőnégyszög szemközti oldalai hosszának összege megegyezik. Ezért feltevésünk hibás, tehát egy érintőtrapéznak mindig van olyan átlója, amelyik az alapokkal legfeljebb ${45}^{\circ }$-os szöget zár be.