Feladat:	B.4276	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Vuchetich Bálint
Füzet:	2011/május, 280 - 281. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Mértani közép, Háromszög nevezetes körei, Magasságvonal, Síkgeometriai bizonyítások, Háromszög területe
Hivatkozás(ok):	Feladatok: 2010/május: B.4276

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.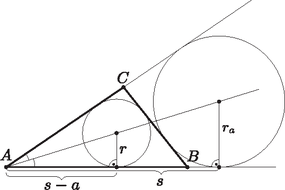   I. megoldás. Jelölje az $ABC$ háromszög $AB=c$ oldalához tartozó magasságát $m_c$, $r_a$ és $r_b$ pedig a $BC=a$, illetve $AC=b$ oldalakhoz hozzáírt körök sugarát. Szokás szerint a háromszög területét jelölje $T$, beírt körének sugarát $r$, kerületének felét pedig $s$. Mivel a magasságoknak egymáshoz képest nincs kitüntetett szerepük, elegendő az $m_c\le \sqrt[]{r_a{r}_b}$ egyenlőtlenséget igazolnunk, ami ekvivalens az $m_c^2\le r_a{r}_b$ egyenlőtlenséggel.     Az $A$ csúcs, a beírt kör középpontja és az $a$ oldalhoz hozzáírt kör középpontja egyaránt az $A$-ból induló belső szögfelezőn helyezkedik el, továbbá e két kör az $AB$ félegyenest az $A$ csúcstól $s-a$, illetve $s$ távolságban érinti, ezért a párhuzamos szelők tételét alkalmazva kapjuk, hogy $r_a:r=s:\left(s-a\right)$, azaz $r_a=\frac{rs}{s-a}$.   Ugyanígy adódik, hogy $r_b=\frac{rs}{s-b}$.   Az $rs=T=\frac{c{m}_c}{2}$ összefüggésből következő $\frac{rs}{m_c}=\frac{c}{2}$ egyenlőséget is felhasználva: $\begin{array}{c}{\displaystyle \frac{r_a{r}_b}{m_c^2}=\frac{r^2{s}^2}{\left(s-a\right)\left(s-b\right)m_c^2}=\frac{c^2}{4\left(s-a\right)\left(s-b\right)}=\frac{c^2}{c^2-{\left(a-b\right)}^2}\ge 1.}\end{array}$ Tehát $r_a{r}_b\ge m_c^2$ mindig teljesül, egyenlőség pedig pontosan akkor áll fenn, ha $a=b$.   II. megoldás. A hozzáírt körök sugarára vonatkozó képlet ismeretében másképp is beláthatjuk a bizonyítandó egyenlőtlenséget: $\begin{array}{c}{\displaystyle m_c=\frac{2T}{c}=\frac{2T}{\left(s-a\right)+\left(s-b\right)}=\frac{2}{\frac{s-a}{T}+\frac{s-b}{T}}=\frac{2}{\frac{1}{r_a}+\frac{1}{r_b}}\le \sqrt[]{r_a{r}_b}\mathrm{,}}\end{array}$ ahol az utolsó lépésben a harmonikus és a mértani közepek közti egyenlőtlenséget alkalmaztuk.