Feladat:	B.4308	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bogár Blanka ,  Hajnal Máté ,  Karl Erik Holter ,  Lenger Dániel ,  Máthé László ,  Varnyú József ,  Viharos Andor
Füzet:	2011/április, 223 - 224. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Körök, Helyvektorok, Középponti és kerületi szögek
Hivatkozás(ok):	Feladatok: 2010/november: B.4308

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Megoldás. Ismert a Feuerbach-körnek az a tulajdonsága, hogy átmegy a háromszög oldalfelező pontjain. Ezt fogjuk kihasználni a bizonyítás során. Az ábra jelölései alapján az $F_i$-k a megfelelő oldalak felezőpontjai, az ezeket összekötő szakaszok középvonalak. Egy háromszög oldalhoz az a középvonal tartozik, amelyik párhuzamos és fele akkora mint az oldal. Emiatt a középvonalak által alkotott háromszög hasonló ez eredetihez és a hasonlóság aránya $\frac{1}{2}$. Tekintsük két, egy átlóhoz tartozó háromszög Feuerbach-körét, például $ABC$ és $ADC$ háromszögekét. Könnyen belátható, hogy ha ennek a két körnek csak egy közös pontja van, akkor az eredeti négyszög átlói felezik egymást, tehát rombuszról van szó, és ekkor az állítás nyilvánvaló. Tehát feltehetjük, hogy a köröknek két metszéspontja van, $F_5$ és $F$. Ha sikerül megmutatnunk, hogy $F$ rajta van $BDC▵$ vagy $ABD▵$ Feuerbach-körén, akkor készen vagyunk, mert hasonló elgondolás alapján a másikén is rajta lesz. 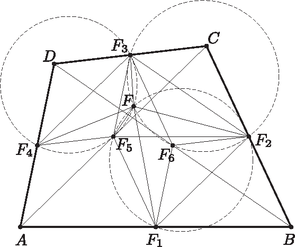    Megmutatjuk, hogy az $F{F}_3{F}_2{F}_6$ négyszög húrnégyszög. Ugyanis ekkor ‐ mivel ebből három pont $BDC▵$ Feuerbach-körén van ‐ a negyedik is azon lesz. A középvonalak tulajdonságai miatt $\begin{array}{c}{\displaystyle F_1{F}_5{F}_2\sphericalangle =ABC\sphericalangle \mathrm{,}\text{valamint}{F}_5{F}_2{F}_1\sphericalangle =CAB\sphericalangle \mathrm{.}}\end{array}$ Ezután a kerületi szögek tétele miatt $F_1{F}_5{F}_2\sphericalangle =F_{1}F{F}_2\sphericalangle$ és $F_5{F}_2{F}_1\sphericalangle =F_{5}F{F}_1\sphericalangle$. Hasonlóan $\begin{array}{c}{\displaystyle F_4{F}_5{F}_3\sphericalangle =ADC\sphericalangle \mathrm{,}\text{valamint}{F}_4{F}_3{F}_5\sphericalangle =DAC\sphericalangle \mathrm{.}}\end{array}$ A kerületi szögek tétele miatt pedig $F_4{F}_5{F}_3\sphericalangle =F_{4}F{F}_3\sphericalangle$ és $F_4{F}_3{F}_5\sphericalangle =F_{4}F{F}_5\sphericalangle$. Ez viszont azt jelenti, hogy ${\displaystyle \begin{array}{cc}\hfill {\displaystyle F_{3}F{F}_2\sphericalangle }& {\displaystyle ={360}^{\circ }-\left(F_{4}F{F}_3\sphericalangle +F_{4}F{F}_5\sphericalangle +F_{5}F{F}_1\sphericalangle +F_{1}F{F}_2\sphericalangle \right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle ={360}^{\circ }-\left(ADC\sphericalangle +DAC\sphericalangle +CAB\sphericalangle +ABC\sphericalangle \right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle ={360}^{\circ }-\left(ADC\sphericalangle +DAB\sphericalangle +ABC\sphericalangle \right)=DCB\sphericalangle \mathrm{.}}\hfill \end{array}}$ Viszont a középvonalak tulajdonságai miatt $F_3{F}_6{F}_2\sphericalangle =DCB\sphericalangle$. Ez azt jelenti, hogy $F_{3}F{F}_2\sphericalangle$ és $F_3{F}_6{F}_2\sphericalangle$ is egy húrhoz, az $F_3{F}_2$-höz tartozó kerületi szögek. Azaz $F{F}_3{F}_2{F}_6$ négyszög húrnégyszög. Ezt kívántuk belátni. Az állítás konkáv négyszögekre is igaz, és hasonló gondolatmenettel látható be.    Hajnal Máté (Kecskeméti Ref. G. 12. évf.)  dolgozata alapján