| Feladat: | B.4288 | Korcsoport: 18- | Nehézségi fok: átlagos |
| Megoldó(k): | Wiandt Zsófia | ||
| Füzet: | 2011/április, 217. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Feladat, Gömb és részei, Kocka, Pitagorasz-tétel alkalmazásai | ||
| Hivatkozás(ok): | Feladatok: 2010/szeptember: B.4288 | ||
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.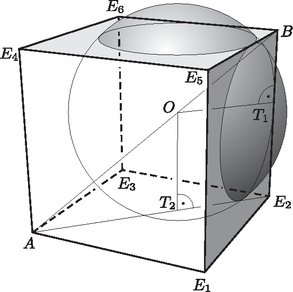 1. ábra 1. ábra 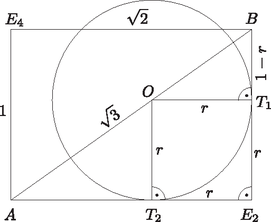 2. ábra 2. ábra Ha a gömbnek az lapon lévő érintési pontját -vel jelöljük, akkor merőleges a lap síkjára, ezért rajta van az testátlónak a lapon lévő merőleges vetületén, az lapátlón. Tekintsük az síkmetszetet (2. ábra). Az négyszögben a , és csúcsoknál derékszög van, továbbá két szomszédos oldala egyenlő hosszú (), ezért a négyszög négyzet, tehát . Ebből közös nevezőre hozva és rendezve kapjuk, hogy , vagyis a keresett sugár: |