Kezdőlap


Feladat:	B.4279	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Ágoston Péter , Ágoston Tamás , Bősze Zsuzsanna , Böőr Katalin , Csere Kálmán , Damásdi Gábor , Dolgos Tamás , Dunay Luca , Éles András , Énekes Péter , Gyarmati Máté , Hegedűs Csaba , Herczeg József , Janzer Olivér , Keresztfalvi Tibor , Márkus Bence , Medek Ákos , Mészáros András , Nagy Róbert , Sieben Bertilla , Strenner Péter , Szabó Attila , Weimann Richárd
Füzet:	2011/április, 213 - 215. oldal		PDF \| MathML
Témakör(ök):	Feladat, Tetraéderek, Térfogat, Ellenpélda, mint megoldási módszer a matematikában
Hivatkozás(ok):	Feladatok: 2010/május: B.4279

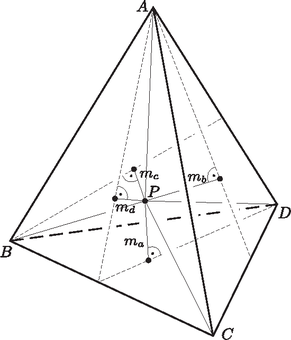
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az

A B C D

tetraéder egy

P

belső pontjának a lapoktól vett távolságait jelölje rendre

m_{a}

m_{b}

m_{c}

és

m_{d}

, az egyes lapok területét pedig

t_{a}

t_{b}

t_{c}

és

t_{d}

. Ekkor az

A B C D

tetraéder térfogata megegyezik a

P B C D

P A C D

P A B D

és

P A B C

tetraéderek térfogatának összegével, vagyis

\begin{matrix} V_{A B C D} = \frac{m_{a} t_{a}}{3} + \frac{m_{b} t_{b}}{3} + \frac{m_{c} t_{c}}{3} + \frac{m_{d} t_{d}}{3} \end{matrix}

P

-től független állandó. Amennyiben mind a négy lap területe egyenlő, s e közös területet

t

jelöli, akkor ebből azt kapjuk, hogy

\begin{matrix} m_{a} + m_{b} + m_{c} + m_{d} = \frac{3 \cdot V_{A B C D}}{t} . \end{matrix}

Tehát minden olyan tetraéderre, amelynek lapjai egyenlő területűek, teljesül, hogy bármely belső pontjának az oldallapoktól vett távolságösszege állandó.
Ilyen tetraédereket könnyen megadhatunk.

^{1}

Vagyis a feladat kérdésére a válasz: az állítás nem igaz.

⁰

1. ábra

2. ábra

II. megoldás. Vegyünk egy megfelelő tetraédert. Ennek lapjainak területe legyen

t_{1}

t_{2}

t_{3}

és

t_{4}

. Vegyünk két benne lévő pontot, ezeknek a lapoktól mért távolsága legyen

d_{1}

d_{2}

d_{3}

és

d_{4}

, illetve

c_{1}

c_{2}

c_{3}

és

c_{4}

.
Bontsuk fel a tetraédert a pontok mentén kisebb tetraéderekre, ekkor a térfogat nem változik:

\begin{matrix} d_{1} t_{1} + d_{2} t_{2} + d_{3} t_{3} + d_{4} t_{4} = c_{1} t_{1} + c_{2} t_{2} + c_{3} t_{3} + c_{4} t_{4} . \end{matrix}

Egyszerűsítsük le a problémát. Legyenek a tetraéder alaplapjai egyenlő nagyságúak:

\begin{matrix} (d_{1} + d_{2} + d_{3} + d_{4}) t & = (c_{1} + c_{2} + c_{3} + c_{4}) t, \\ d_{1} + d_{2} + d_{3} + d_{4} & = c_{1} + c_{2} + c_{3} + c_{4} . \end{matrix}

Ha az alaplapok egyenlő nagyságúak, akkor bármely belső pontnak a lapoktól mért távolságösszege egyenlő. Keressünk azonos területű lapokból álló tetraédereket.
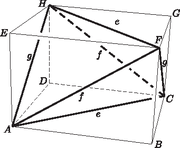
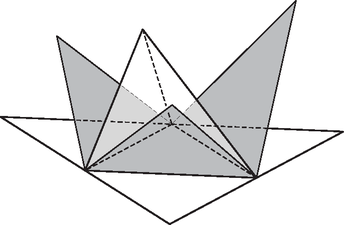
Vegyünk egy tetszőleges háromszöget, rajzoljuk meg a középvonalait, és hajtsuk fel azokat a háromszögeket, melyeknek oldalai közül kettő érintkezik a háromszög eredeti oldalával, a harmadik pedig a háromszög egy középvonala (2. ábra). A felhajtott háromszögek és a megmaradt alap egy tetraédert határoznak meg. Minden lap egybevágó, tehát területük megegyezik. Ezzel a feladat alapállítása nem igaz, mivel találtunk egy ellenpéldát.

Gyarmati Máté(Pécs, Leőwey Klára G., 10. évf.)

Megjegyzés. Megmutatható, hogy ha egy tetraéder lapjai egyenlő területűek, akkor a lapok egybevágóak is. Ebből az is következik, hogy a tetraédert a megoldásban leírt módon kaphatjuk meg valamely téglatestből (vagyis a tetraéder bennfoglaló paralelepipedonja téglatest). Ennek bizonyítása megtalálható például Reiman I.: Fejezetek az elemi geometriából című gimnáziumi tankönyvének 9. fejezetében.

⁰

^{1}

Ha például a lapok egybevágóak, akkor nyilván teljesítik a feltételt. Legyen

A B C D E F G H

egy téglatest, aminek

A C

és

F H

két párhuzamos lapon lévő, egy egymással nem párhuzamos lapátlója. Ekkor, ha a téglatest egy csúcsban találkozó három lapja átlóinak hossza

e

f

és

g

, akkor az

A C F H

tetraéder minden lapjának pontosan egy

e

, egy

f

és egy

g

hosszúságú éle van. Ha a téglatest nem kocka, akkor lapátlói közt vannak különböző hosszúságúak, ezért ekkor az

A C F H

tetraéder nem szabályos.