Feladat:	B.4258	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	2011/április, 209 - 210. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Síkbeli ponthalmazok távolsága, Pitagorasz-tétel alkalmazásai, Sokszögek súlypontjának koordinátái, Osztópontok koordinátái
Hivatkozás(ok):	Feladatok: 2010/március: B.4258

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Az $A$, $B$, $C$ pontokat az $e$ egyenesre merőlegesen vetítve, a kapott pontokat jelölje rendre $A_1$, $B_1$, $C_1$. Pithagorasz tétele szerint $\begin{array}{c}{\displaystyle P{A}^2+2P{B}^2+3P{C}^2=\left(P{A}_1^2+2P{B}_1^2+3P{C}_1^2\right)+\left(A{A}_1^2+2B{B}_1^2+3C{C}_1^2\right)\mathrm{.}}\end{array}$ Az $e$ egyenest a számegyenessel azonosítva, az $A_1$, $B_1$, $C_1$ pontok koordinátája legyen rendre $a$, $b$, $c$, az ismeretlen $P$ pont koordinátája pedig $x$. Mivel $A{A}_1^2+2B{B}_1^2+3C{C}_1^2$ állandó, a szóban forgó összeg akkor a legkisebb, amikor $\begin{array}{c}{\displaystyle P{A}_1^2+2P{B}_1^2+3P{C}_1^2={\left(x-a\right)}^2+2{\left(x-b\right)}^2+3{\left(x-c\right)}^2}\end{array}$ értéke a lehető legkisebb. Ezt az $x$-ben másodfokú kifejezést teljes négyzetté kiegészítve $\begin{array}{c}{\displaystyle 6{\left(x-\frac{a+2b+3c}{6}\right)}^2+\left(a^2+2b^2+3c^2\right)-\frac{{\left(a+2b+3c\right)}^2}{6}}\end{array}$ adódik. Ez nyilván akkor a legkisebb, ha $\begin{array}{c}{\displaystyle x=\frac{a+2b+3c}{6}=\frac{\frac{a+c}{2}+b+c}{3}\mathrm{.}}\end{array}$ Ekkor a $P$ pont éppen a $BCD$ háromszög súlypontjának az $e$ egyenesre eső merőleges vetülete, ahol $D$ az $AC$ szakasz felezőpontját jelöli.   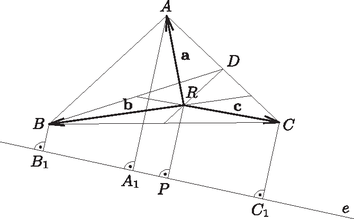II. megoldás. Legyen $R$ olyan pont, melyből induló $\overrightarrow{RA}=\text{<span style="font-weight: bold;">a</span>}$, $\overrightarrow{RB}=\text{<span style="font-weight: bold;">b</span>}$ és $\overrightarrow{RC}=\text{<span style="font-weight: bold;">c</span>}$ vektorokra teljesül az $\text{<span style="font-weight: bold;">a</span>}+2\text{<span style="font-weight: bold;">b</span>}+3\text{<span style="font-weight: bold;">c</span>}=\text{<span style="font-weight: bold;">0</span>}$ összefüggés, továbbá legyen $\overrightarrow{RP}=\text{<span style="font-weight: bold;">p</span>}$. Azt, hogy ilyen $R$ pont létezik, később bizonyítjuk. Ekkor ${\displaystyle \begin{array}{c}\hfill {\displaystyle P{A}^2+2P{B}^2+3P{C}^2={\left(\text{<span style="font-weight: bold;">a</span>}-\text{<span style="font-weight: bold;">p</span>}\right)}^2+2{\left(\text{<span style="font-weight: bold;">b</span>}-\text{<span style="font-weight: bold;">p</span>}\right)}^2+3{\left(\text{<span style="font-weight: bold;">c</span>}-\text{<span style="font-weight: bold;">p</span>}\right)}^2=}\hfill \\ \hfill {\displaystyle =\left({\text{<span style="font-weight: bold;">a</span>}}^2+2{\text{<span style="font-weight: bold;">b</span>}}^2+3{\text{<span style="font-weight: bold;">c</span>}}^2\right)+6{\text{<span style="font-weight: bold;">p</span>}}^2-2\text{<span style="font-weight: bold;">p</span>}\left(\text{<span style="font-weight: bold;">a</span>}+2\text{<span style="font-weight: bold;">b</span>}+3\text{<span style="font-weight: bold;">c</span>}\right)=\left({\text{<span style="font-weight: bold;">a</span>}}^2+2{\text{<span style="font-weight: bold;">b</span>}}^2+3{\text{<span style="font-weight: bold;">c</span>}}^2\right)+6{\text{<span style="font-weight: bold;">p</span>}}^2\mathrm{.}}\hfill \end{array}}$     Az $\text{<span style="font-weight: bold;">a</span>}$, $\text{<span style="font-weight: bold;">b</span>}$ és $\text{<span style="font-weight: bold;">c</span>}$ rögzített vektorok, ezért a kifejezés értéke akkor a legkisebb, ha ${\text{<span style="font-weight: bold;">p</span>}}^2$ értéke a lehető legkisebb. Ez akkor következik be, amikor az $RP$ szakasz hossza minimális, azaz a keresett pont éppen $R$-nek az $e$ egyenesen lévő merőleges vetülete. Meg kell még határoznunk az $\text{<span style="font-weight: bold;">a</span>}+2\text{<span style="font-weight: bold;">b</span>}+3\text{<span style="font-weight: bold;">c</span>}=\text{<span style="font-weight: bold;">0</span>}$ összefüggésnek eleget tevő $R$ pontokat. Megmutatjuk, hogy pontosan egy ilyen tulajdonságú pont van, s ez annak a $BCD$ háromszögnek a súlypontja, melynek $D$ csúcsa az $AC$ szakasz felezőpontja. Ha ugyanis $\overrightarrow{RD}=\text{<span style="font-weight: bold;">d</span>}$, akkor a súlypont tulajdonságaiból következően $\text{<span style="font-weight: bold;">b</span>}+\text{<span style="font-weight: bold;">c</span>}+\text{<span style="font-weight: bold;">d</span>}=\text{<span style="font-weight: bold;">0</span>}$, $D$ felezőpont volta miatt pedig $\text{<span style="font-weight: bold;">d</span>}=\left(\text{<span style="font-weight: bold;">a</span>}+\text{<span style="font-weight: bold;">c</span>}\right)/2$, vagyis $\begin{array}{c}{\displaystyle \text{<span style="font-weight: bold;">0</span>}=\text{<span style="font-weight: bold;">b</span>}+\text{<span style="font-weight: bold;">c</span>}+\text{<span style="font-weight: bold;">d</span>}=\text{<span style="font-weight: bold;">b</span>}+\text{<span style="font-weight: bold;">c</span>}+\frac{\text{<span style="font-weight: bold;">a</span>}+\text{<span style="font-weight: bold;">c</span>}}{2}=\frac{\text{<span style="font-weight: bold;">a</span>}+2\text{<span style="font-weight: bold;">b</span>}+3\text{<span style="font-weight: bold;">c</span>}}{2}\mathrm{.}}\end{array}$ Tehát ez a pont eleget tesz a követelménynek. Ha valamely $T$ pontra teljesül, hogy $\overrightarrow{TA}+2\overrightarrow{TB}+3\overrightarrow{TC}=\text{0}$, akkor ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \text{0}}& {\displaystyle =\overrightarrow{TA}+2\overrightarrow{TB}+3\overrightarrow{TC}=\left(\overrightarrow{TR}+\overrightarrow{RA}\right)+2\left(\overrightarrow{TR}+\overrightarrow{RB}\right)+3\left(\overrightarrow{TR}+\overrightarrow{RC}\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =6\overrightarrow{TR}+\text{a}+2\text{b}+3\text{c}=6\overrightarrow{TR}\mathrm{,}}\hfill \end{array}}$ tehát $\overrightarrow{TR}=\text{0}$, azaz $T$ egybeesik $R$-rel.   Megjegyzés. Ha adott egy $ABC$ háromszög, valamint az $\alpha$, $\beta$, $\gamma$ valós számok, melyekre $\alpha +\beta +\gamma \ne 0$ teljesül, akkor megmutatható,   hogy pontosan egy olyan $P$ pont van, melyre fennáll az $\alpha \overrightarrow{PA}+\beta \overrightarrow{PB}+\gamma \overrightarrow{PC}=\text{0}$ összefüggés, másrészt pedig a háromszög síkjának bármely pontjához létezik olyan $\left(\alpha \mathrm{,}\beta \mathrm{,}\gamma \right)$ skalárszorzó erejéig egyértelmű, rendezett számhármas, melyre teljesül az összefüggés. Az érdeklődő olvasó ennek részletes leírását megtalálja például Hajós Gy.: Bevezetés a geometriába című könyvében a baricentrikus koordinátákról szóló 35.5. részben.