Feladat:	B.4256	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	2011/április, 207 - 209. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Másodfokú (és arra visszavezethető) egyenletek, Trigonometrikus egyenletek, Trigonometriai azonosságok, Háromszög nevezetes vonalai
Hivatkozás(ok):	Feladatok: 2010/március: B.4256

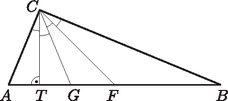
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Megoldás. Tegyük fel, hogy az $ABC$ háromszög $C$ csúcsánál lévő szögét négy egyenlő részre osztja a $CT$ magasságvonal, a $CF$ súlyvonal és a $CG$ szögfelező. Jelöljük a háromszög oldalait és szögeit a szokásos módon $a$, $b$, $c$, illetve $\alpha$, $\beta$, $\gamma$-val. Ha $a=b$, akkor a $T$, $F$ és $G$ pontok egybeesnek. Tehát $a\ne b$. Az oldalak szimmetrikus szerepe miatt feltehetjük, hogy $a>b$ teljesül. Mivel $T$ az $AB$ oldal belső pontja, $\alpha <{90}^{\circ }$ és $\beta <{90}^{\circ }$ is teljesül, továbbá $a>b$ miatt $\alpha >\beta$, amiből viszont $ACT\sphericalangle ={90}^{\circ }-\alpha <{90}^{\circ }-\beta =BCT\sphericalangle$ következik.     Ezért az $ABC$ háromszög $C$ csúcsához tartozó szögfelező a $BCT$ szögtartományban halad, tehát $T$ az $AG$ szakasz belső pontja. A szögfelezőtétel következménye szerint $AG=\frac{bc}{a+b}<\frac{c}{2}$, ezért $G$ az $AF$ szakasz belső pontja. Vagyis az $A$, $T$, $G$, $F$, $B$ pontok ebben a sorrendben követik egymást. A hasonlóságok nem változtatják meg a szögeket, ezért feltehetjük, hogy $CT=1$, továbbá az egyszerűség kedvéért vezessük be a $\delta =\gamma /4$ jelölést. Ekkor $ACT\sphericalangle =TCG\sphericalangle =GCF\sphericalangle =FCB\sphericalangle =\delta$, ezért $AT=TG=\text{tg}\delta$, $TF=\text{tg}2\delta$ és $TB=\text{tg}3\delta$, vagyis $\begin{array}{c}{\displaystyle \text{tg}\delta +\text{tg}2\delta =AT+TF=AF=FB=TB-TF=\text{tg}3\delta -\text{tg}2\delta \mathrm{.}}\end{array}$ Vezessük be a $z=\text{tg}\delta$ jelölést és alkalmazzuk a tangens függvény addíciós képletét, mely szerint: $\begin{array}{c}{\displaystyle \text{tg}2\delta =\frac{2\text{tg}\delta }{1-\text{tg}{}^2\delta }=\frac{2z}{1-z^2}\text{és}\text{tg}3\delta =\frac{\text{tg}\delta +\text{tg}2\delta }{1-\text{tg}\delta \text{tg}2\delta }=\frac{3z-z^3}{1-3z^2}\mathrm{,}}\end{array}$ a következő egyenletet kapjuk: $\begin{array}{c}{\displaystyle z+\frac{4z}{1-z^2}=\frac{3z-z^3}{1-3z^2}\mathrm{.}}\end{array}$ Hozzunk közös nevezőre: $\begin{array}{c}{\displaystyle \left(5z-z^3\right)\left(1-3z^2\right)=\left(3z-z^3\right)\left(1-z^2\right)}\end{array}$ egyenlet adódik, amit $z\ne 0$-val osztva majd rendezve a $z^4-6z^2+1=0$ egyenletet kapjuk, ami $z^2$-re nézve másodfokú. Ennek megoldásai a megoldóképlet alapján, valamint a $3\pm \sqrt[]{8}={\left(\sqrt[]{2}\pm 1\right)}^2$ összefüggést felhasználva: $\begin{array}{c}{\displaystyle z=\pm \left(\sqrt[]{2}\pm 1\right)\mathrm{.}}\end{array}$ Mivel $0^{\circ }<\delta <{45}^{\circ }$, csak a $0<z<1$ egyenlőtlenségeknek eleget tevő $z=\sqrt[]{2}-1$ megoldás adhat megfelelő háromszöget. Ebből kapjuk, hogy $\begin{array}{c}{\displaystyle \delta =\text{arctg}\left(\sqrt[]{2}-1\right)=22\mathrm{,}{5}^{\circ }\mathrm{.}}\end{array}$ Mivel $\gamma =4\delta$, azért a háromszög derékszögű. Bármely derékszögű háromszögben a derékszögű csúcshoz tartozó magasságvonalnak a befogókkal bezárt szögei megegyeznek a háromszög hegyesszögeivel, tehát csak olyan derékszögű háromszög tehet eleget a feladat feltételeinek, melynek egyik hegyesszöge $22\mathrm{,}{5}^{\circ }$. Ha az $ABC$ háromszögben ez teljesül, akkor $\begin{array}{c}{\displaystyle AGC\sphericalangle ={180}^{\circ }-\left(CAG\sphericalangle +ACG\sphericalangle \right)={180}^{\circ }-\left(67\mathrm{,}{5}^{\circ }+{45}^{\circ }\right)=67\mathrm{,}{5}^{\circ }=CAG\sphericalangle \mathrm{,}}\end{array}$ tehát az $AGC$ háromszög egyenlő szárú, azaz $CT$ felezi az $ACG$ szöget, s ezért negyedeli az $ACB$ szöget. Mivel a derékszögű háromszög köré írható kör középpontja az átfogó felezőpontja, az $FBC$ háromszög is egyenlő szárú, tehát $FCB\sphericalangle =FBC\sphericalangle =22\mathrm{,}{5}^{\circ }=\frac{{90}^{\circ }}{4}$, vagyis a $C$-hez tartozó súlyvonal is negyedeli az ott lévő szöget. Tehát a feladat feltételeinek pontosan azok a derékszögű háromszögek tesznek eleget, amelyeknek egyik hegyesszöge $22\mathrm{,}{5}^{\circ }$.