Kezdőlap


Feladat:	B.4238	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Klincsik Gergely , Neukirchner Elisabeth
Füzet:	2011/február, 83 - 84. oldal		PDF \| MathML
Témakör(ök):	Feladat, Parabola, mint mértani hely, Két pont távolsága, szakasz hosszúsága, Pont és egyenes távolsága, Koordináta-geometria
Hivatkozás(ok):	Feladatok: 2010/január: B.4238

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Megmutatjuk, hogy a görbe minden pontja ugyanolyan távol van az $F (\frac{1}{2}; \frac{1}{2})$ ponttól, mint az $X + Y = 0$ egyenletű $v$ egyenestől, vagyis illeszkedik arra a parabolára, amelynek fókuszpontja $F$ , vezéregyenese pedig 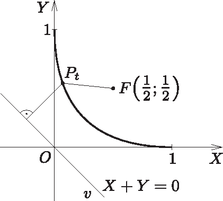$v$ .
Tudjuk, hogy valamely $P (x_{0}; y_{0})$ pontnak az $A X + B Y + C = 0$ egyenletű $e$ egyenestől való távolsága

\begin{matrix} d (P, e) = \frac{| A x_{0} + B y_{0} + C |}{\sqrt[]{A^{2} + B^{2}}} . \end{matrix}

Esetünkben tehát

d (P, v) = | x_{0} + y_{0} | / \sqrt[]{2}

, a

P F

szakasz hossza pedig a két pont távolságát megadó képlet szerint:

\begin{matrix} P F = \sqrt[]{{(x_{0} - \frac{1}{2})}^{2} + {(y_{0} - \frac{1}{2})}^{2}} . \end{matrix}

Mivel a vizsgált görbe minden pontja az első síknegyedben van, azért ha a görbe valamely

P_{t}

pontjának első koordinátája

t

, akkor

0 \leq t \leq 1

teljesül, és a pont koordinátái

(t, {(1 - \sqrt[]{t})}^{2})

.
A

d (P_{t}, v) = F P_{t}

feltétel a görbe pontjaira ekvivalens a

{(d (P_{t}, v))}^{2} = F P_{t}^{2}

, vagyis a

\begin{matrix} \frac{{(t + {(1 - \sqrt[]{t})}^{2})}^{2}}{2} = {(t - \frac{1}{2})}^{2} + {({(1 - \sqrt[]{t})}^{2} - \frac{1}{2})}^{2} \end{matrix}

egyenlőség fennállásával. A négyzetre emeléseket elvégezve és 4-gyel szorozva ebből azonos átalakítások után a

\begin{matrix} 2 (1 + 4 t^{2} + 8 t - 4 t \sqrt[]{t} - 4 \sqrt[]{t}) = (4 t^{2} + 1 - 4 t) + (4 t^{2} + 12 t + 1 - 16 t \sqrt[]{t} + 8 \sqrt[]{t}) . \end{matrix}

azonosságot kapjuk.
Ezzel állításunkat beláttuk.

II. megoldás. A görbe egyenlete nem változik, ha

X

-et és

Y

-t felcseréljük. Ez azt jelenti, hogy a görbe szimmetrikus az

Y = X

egyenletű egyenesre, a koordinátatengelyek szögfelezőjére. Egy parabola egyenlete olyan koordinátarendszerben ölti a legegyszerűbb alakot, melynek egyik tengelye egybeesik a parabola szimmetriatengelyével. Ezért érdemes elforgatnuk az eredeti koordinátarendszert az origója körül úgy, hogy az új rendszer egyik tengelye legyen a régi

Y = X

egyenes, azaz pl.

{+ 315}^{\circ}

-kal.
Ha az új koordinátákat

X'

és

Y'

jelöli, akkor a transzformációs képletek szerint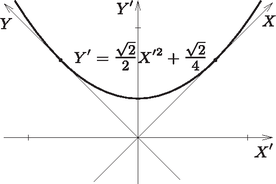

\begin{matrix} X & = cos 315^{\circ} X' - sin 315^{\circ} Y' = \frac{\sqrt[]{2}}{2} X' + \frac{\sqrt[]{2}}{2} Y', \\ Y & = sin 315^{\circ} X' + cos 315^{\circ} Y' = \frac{- \sqrt[]{2}}{2} X' + \frac{\sqrt[]{2}}{2} Y' . \end{matrix}

Tehát a görbe egyenlete az új koordinátarendszerben

\begin{matrix} \sqrt[]{\frac{\sqrt[]{2}}{2} (X' + Y')} + \sqrt[]{\frac{\sqrt[]{2}}{2} (Y' - X')} = 1. \end{matrix}

Mivel mindkét oldal nemnegatív, azért ugyanannak a görbének az egyenletét kapjuk, ha ezt az egyenletet négyzetre emeljük, majd rendezzük:

\begin{matrix} 2 \sqrt[]{Y'^{2} - X'^{2}} = \sqrt[]{2} - 2 Y' . \end{matrix}

Ha most ismét négyzetre emelünk, akkor a kapott egyenletet az eredeti görbe minden pontjának koordinátái kielégítik (és a négyzetre emelés miatt esetleg más pontok koordinátái is):

\begin{matrix} 4 Y'^{2} - X'^{2} = 2 + 4 Y'^{2} - 4 \sqrt[]{2} Y' . \end{matrix}

Tehát az eredeti görbe minden pontja rajta van az

\begin{matrix} Y' = \frac{\sqrt[]{2}}{2} X'^{2} + \frac{\sqrt[]{2}}{4} \end{matrix}

egyenletű parabolán, s ezzel az állítást beláttuk.