Kezdőlap


Feladat:	B.4264	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Uray Marcell János , Zsakó András
Füzet:	2011/január, 22 - 23. oldal		PDF \| MathML
Témakör(ök):	Feladat, Magasságpont, Körülírt kör középpontja, Középponti és kerületi szögek, Húrnégyszögek
Hivatkozás(ok):	Feladatok: 2010/április: B.4264

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Mivel a háromszög $C$ csúcsánál lévő szög $120^{\circ}$ , a kerületi szögek tétele alapján az $F$ pontból az $A B$ szakasz $120^{\circ}$ -os szögben látszik. Ennek a szögnek a szögfelezőjén van rajta az $O$ pont, mivel $F$ az $A B$ ív felezőpontja, ezért $A F O ∢ = O F B ∢ = 60^{\circ}$ . Az $A F O$ és $O F B$ háromszögek egyenlő szárúak és van $60^{\circ}$ -os szögük, ezért szabályosak, tehát 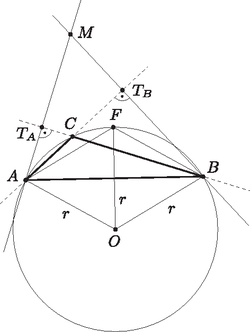$A F = F B = r$ .
Az $M T_{A} C T_{B}$ négyszög húrnégyszög, mert két szemközti szöge derékszög (1. ábra).

1. ábra

A húrnégyszögek tétele alapján

A M B + T_{A} C T_{B} = 180^{\circ}

. Az utóbbi megegyezik

A C B ∢ = 120^{\circ}

-kal, mivel csúcsszögek, ezért

A M B ∢ = 60^{\circ}

. Ugyanakkor

A O B ∢ = 2 \cdot 60^{\circ} = 120^{\circ}

, ezért az

A M B O

négyszög is húrnégyszög. Az

A O B

háromszög körülírt körének középpontja

F

, mert

F A = F O = F B = r

.
Mivel

A M B O

húrnégyszög, az

M

pont rajta van az

A O B

háromszög körülírt körén, amiből következik, hogy

M F = F O = r

, és ezt kellett bizonyítani.

II. megoldás. Mivel

M

a magasságpont és

O

A B C

háromszög köré írt kör középpontja, tudjuk, hogy

\vec{O M} = \vec{O A} + \vec{O B} + \vec{O C}

.
Vegyük észre, hogy az

O A F B

négyszög rombusz, ugyanis a háromszögben a

C

csúcsnál lévő szög

120^{\circ}

, így

A O B ∢

120^{\circ}

, mert a

C

pontból az

A F B

ív kiegészítő ívét látjuk

120^{\circ}

alatt, így az a középpontból

2 \cdot 120^{\circ} = 240^{\circ}

alatt látszik, vagyis

A O B ∢ = 360^{\circ} - 240^{\circ} = 120^{\circ}

, és

F

-ből az

A B

húr ugyanakkora szög alatt látszik, mint

C

-ből. Ebből következik, hogy

O A F

és

O F B

egyenlő oldalú háromszögek.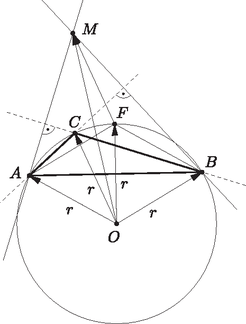

2. ábra

Ha az

O A F B

négyszög rombusz, akkor paralelogramma is, így

\vec{O A} + \vec{O B} = \vec{O F}

. A 2. ábráról látható, hogy

\vec{O M} = \vec{O F} + \vec{F M}

, így

\begin{matrix} \vec{O M} = \vec{O A} + \vec{O B} + \vec{O C} = \vec{O F} + \vec{O C} = \vec{O F} + \vec{F M}, \end{matrix}

amiből következik, hogy

\vec{O C} = \vec{F M}

. Mivel

O F

hossza egyenlő a kör sugarával, az

O F

távolság egyenlő az

O C

távolsággal, vagyis

O F = F M