Kezdőlap


Feladat:	B.4441	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Dinev Georgi
Füzet:	2013/december, 540 - 541. oldal		PDF \| MathML
Témakör(ök):	Feladat, Térgeometriai bizonyítások, Vektorok lineáris kombinációi, Vektorok skaláris szorzata, Vektorok vektoriális szorzata
Hivatkozás(ok):	Feladatok: 2012/március: B.4441

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.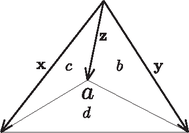

Megoldás. Jelölje a

d

területű lappal szemközti csúcsból a másik három csúcsba mutató vektort

x

y

és

z

. Feltehetjük, hogy a három vektor ebben a sorrendben jobbrendszert alkot. Ekkor a vektoriális szorzás definíciójából következik, hogy

\begin{matrix} 2 a = | x \times y |, 2 b = | y \times z | és 2 c = | z \times x | . \end{matrix}

Ugyanakkor a

d

területű háromszöglap két oldalvektora

z - x

és

y - x

(1. ábra), ezért a vektoriális szorzásnak az összeadásra vonatkozó disztributivitása valamint a tetszőleges

u

és

v

vektorokra fennálló

u \times u = 0

és

u \times v = - v \times u

azonosságok miatt

\begin{matrix} 2 d = | (z - x) \times (y - x) | = | - x \times y - y \times z - z \times x | . \end{matrix}

x \times y

y \times z

és

z \times x

vektorok merőlegesek a tetraéder megfelelő lapjaira, ezért az általuk bezárt szögek éppen a lapok által bezárt szögek kiegészítő szögei, azaz rendre

180^{\circ} - γ

180^{\circ} - α

és

180^{\circ} - β

1. ábra

(Ezt az ismert összefüggést könnyen beláthatjuk. Ha a tetraéder két lapjának közös éle a

k

szakasz, ennek egy tetszőleges belső pontja

P

, a

k

-ra merőleges

S

sík pedig a lapokat az

e

és

f

szakaszokban metszi (2. ábra), akkor az e két szakasz által bezárt szög éppen a két lap szöge (ez a szög tompaszög is lehet, ellentétben a két lap síkjainak hajlásszögével).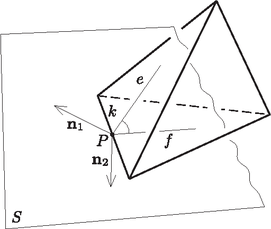

2. ábra

A lapok normálvektorai,

n_{1}

és

n_{2}

benne vannak az

S

síkban, s mivel a normálvektorok az adott síkok minden egyenesére merőlegesek, azért

n_{1} ⊥ e

és

n_{2} ⊥ f

(3. ábra), amiből azonnal adódik a szögekre vonatkozó állítás.) Ezért a vektorok skaláris szorzatának tulajdonságait felhasználva kapjuk, hogy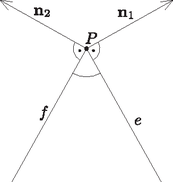

\begin{matrix} 4 d^{2} & = & {(- x \times y - y \times z - z \times x)}^{2} = \\ = & {(x \times y)}^{2} + {(y \times z)}^{2} + {(z \times x)}^{2} + \\ + 2 (x \times y) (y \times z) + 2 (y \times z) (z \times x) + 2 (z \times x) (x \times y) = \\ = & 4 (a^{2} + b^{2} + c^{2} + 2 a b \cdot cos (180^{\circ} - γ) + 2 b c \cdot cos (180^{\circ} - α) + \\ + 2 c a \cdot cos (180^{\circ} - β)) = \\ = & 4 (a^{2} + b^{2} + c^{2} - 2 a b \cdot cos γ - 2 b c \cdot cos α - 2 c a \cdot cos β), \end{matrix}

amiből

4

-gyel való osztás után adódik a bizonyítandó állítás.

3. ábra

Megjegyzések. 1. A feladat állítását nevezhetjük tetraéderekre vonatkozó koszinusztételnek, mert a ,,szokásos'' koszinusztétel természetes általánosítása.
2. A megoldás során beláttuk azt az ismert állítást is, mely szerint ha egy tetraéder minden lapjára egy olyan vektort állítunk, amely az adott lapra merőleges, kifelé mutat, hossza pedig megegyezik az adott lap területével, akkor az így kapott négy vektor összege

0