Feladat: B.4426 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Nagy Anna Noémi 
Füzet: 2013/május, 285 - 286. oldal  PDF  |  MathML 
Témakör(ök): Feladat, Térgeometriai számítások trigonometria nélkül, Pitagorasz-tétel alkalmazásai, Hossz, kerület
Hivatkozás(ok):Feladatok: 2012/február: B.4426

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Először megmutatjuk, hogy T a BCD háromszög magasságpontja. Mivel AT merőleges a BCD síkra, merőleges annak minden egyenesére, így CD-re is. Mivel CD a tetraéder vele szemközti AB élére is merőleges, azért CD az ABT síkra is merőleges, merőleges az abban lévő BT egyenesre is, vagyis BT magasságvonal a BCD háromszögben (1. ábra). A tetraéder másik két szemközti élpárjának merőlegességét felhasználva ugyanígy látható be, hogy CT és DT is magasságvonalak a BCD háromszögben, tehát T a háromszög magasságpontja. Mivel BCD hegyesszögű, azt is tudjuk, hogy T a háromszög belső pontja.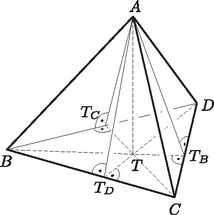


 

1. ábra
 

 
Legyen TB a BT magasságvonal és a CD szakasz metszéspontja. Mivel az ATB szakasz is benne van az ABT síkban, erre is merőleges a CD egyenes, tehát ATB megegyezik az ACD háromszög A csúcshoz tartozó magasságvonalával. Ugyanígy láthatjuk be, hogy ha TC, illetve TD a BCD háromszög C-ből, illetve D-ből induló magasságvonalainak talppontjai, akkor CTC⊥BD és DTD⊥BC.
Pont és egyenes között a legrövidebb távolság a pontból az egyenesre bocsátott merőleges szakasz hossza, a TB, TC és TD pontok pedig a megfelelő háromszögoldalak belső pontjai, ezért az A-t T-vel összekötő töröttvonalak közül az ABC lapon áthaladó legrövidebbnek a hossza ATD+TDT, az ACD, illetve ABD lapokon áthaladó legrövidebbnek a hossza pedig ATB+TBT, illetve ATC+TCT. E három töröttvonal közül kell tehát a legrövidebbet kiválasztanunk.
Az ATTB, ATTC és ATTD olyan derékszögű háromszögek, amelyeknek egyik befogója, AT, közös. Ezért közülük annak a kerülete a legkisebb, amelyiknek a másik befogója a legrövidebb. A legrövidebb befogó nyilván abban a háromszögben van, amelyikben a TATB∢, TATC∢ és TATD∢ közül a legkisebb található. Ezek a szögek éppen 90∘-ra egészítik ki a BCD sík és az ACD, ABD, illetve ABC síkok hajlásszögét. Vagyis a legrövidebb töröttvonal azon az oldallapon fut, amelyik a tetraéder BCD lapjával a legnagyobb szöget zárja be.
Tehát a legrövidebb AT töröttvonalat úgy kapjuk, hogy kiválasztjuk az ABC, ACD és ABD lapok közül azt, amelyik a legnagyobb szöget zárja be a BCD lappal (ha több ilyen lap van, akkor ezek egyikét), majd ennek a lapnak az A-ból induló magasságának talppontját összekötjük A-val is és T-vel is.
 

Megjegyzés. A TTB, TTC és TTD szakaszok közül a legkisebb kiválasztása tulajdonképpen azt jelenti, hogy a BCD hegyesszögű háromszögben meg kell találnunk azt az oldalt, amelyikhez legközelebb van a háromszög T magasságpontja. Ennek a feladatnak a megoldása azonnal adódik a következő észrevételből.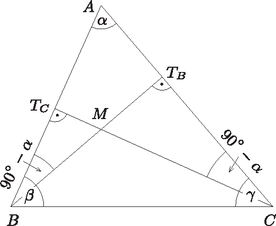
 

 
2.ábra
 

Hegyesszögű háromszög magasságpontja a háromszög bármely két oldala közül a rövidebbhez van közelebb.
 
Ennek belátása a 2. ábrán látható jelölések alapján egyszerű: Mivel ACTC∢=ABTB∢=90∘-α,
MTB=CTBtg(90∘-α)=(BCcosγ)tg(90∘-α)=acosγtg(90∘-α),MTC=BTCtg(90∘-α)=(BCcosβ)tg(90∘-α)=acosβtg(90∘-α).
Tudjuk, hogy egy háromszögben nagyobb szöggel szemben nagyobb oldal van, ezért ha b>c, akkor β>γ, azaz cosγ>cosβ, tehát MTB>MTC.

 
Visszatérve feladatunkra tehát a legrövidebb töröttvonalat úgy kapjuk, hogy kiválasztjuk a BCD háromszög legrövidebb oldalát (ha több ilyen oldal van, akkor ezek egyikét), majd az ezen az oldalon lévő magasságtalppontot összekötjük A-val is és T-vel is.