Számozzuk meg a négyzet sorait fentről lefelé, oszlopait pedig balról jobbra 1-től 23-ig.
Színezzük ki először úgy a négyzetet, hogy a páratlan számú sorok legyenek feketék, és a párosak pedig fehérek. Ekkor $12\times 23$ db fekete és $11\times 23$ db fehér mező van. Minden $3\times 3$-as négyzet vagy 3 db, vagy 6 db fekete mezőt fed le, és minden $2\times 2$-es négyzet pontosan 2 db-ot. Emiatt a $3\times 3$-as négyzetek által lefedett fekete és fehér mezők számának különbsége osztható 3-mal, valamint a $2\times 2$-es négyzetek által lefedett fekete és fehér mezők számának különbsége is osztható 3-mal. Tudjuk, hogy az összes fekete és fehér mezők számának különbsége 23. Ha az $1\times 1$-es négyzet fekete mezőn van, akkor a megmaradó fekete és a fehér mezők számának különbsége 22, ami nem osztható 3-mal, tehát a maradékot nem tudjuk lefedni $2\times 2$-es és $3\times 3$-as négyzetekkel. Emiatt az $1\times 1$-es négyzet csak fehér mezőn lehet, vagyis páros sorban.
Most színezzük ki a $23\times 23$-as táblát úgy, hogy a páratlan számú oszlopok legyenek feketék, a párosak pedig fehérek. Ekkor a fenti gondolatmenethez hasonló módon kapjuk, hogy az $1\times 1$-es négyzet csak fehér mezőn lehet, vagyis csak páros sorszámú oszlopban.
Most úgy színezzük ki a $23\times 23$-as táblát, hogy azok a sorok, melyeknek sorszáma 3-mal osztható legyenek pirosak, a többi sor pedig legyen kék. Ekkor minden $3\times 3$-as négyzet 6 db kék mezőt fed le, és minden $2\times 2$-es négyzet vagy 2 db vagy 4 db kék mezőt fed le. Tehát minden $3\times 3$-as és $2\times 2$-es négyzet páros sok kék mezőt fed le. Tudjuk, hogy összesen $16\times 23$, vagyis páros számú kék mező van. Ha az $1\times 1$-es négyzet kék mezőn van, akkor páratlan számú kék mező marad, tehát nem tudjuk a maradékot $2\times 2$-es és $3\times 3$-as négyzetekkel lefedni. Emiatt az $1\times 1$-es négyzet csak piros mezőn lehet, 3-mal osztható sorszámú sorban.
Most színezzük ki úgy a $23\times 23$-as táblát, hogy azok az oszlopok, melyeknek sorszáma 3-mal osztható legyenek pirosak, a többi sor pedig legyen kék. Akkor a fenti gondolatmenethez hasonlóan kapjuk, hogy az $1\times 1$-es négyzet csak piros mezőn lehet, 3-mal osztható sorszámú oszlopban.
Tehát az $1\times 1$-es négyzet csak 6-tal osztható sorszámú oszlopban és 6-tal osztható sorszámú sorban lehet, vagyis összesen 9 helyen lehet a táblán.
Most megmutatjuk, hogy ez a 9 lehetőség meg is valósítható.
Először megmutatjuk, hogy ha $k\ge 1$, akkor $\left(2k+1\right)\times 6n$-es téglalapot le lehet fedni $2\times 2$-es és $3\times 3$-as négyzetekkel. Egy $3\times 6n$-es téglalapot le lehet fedni csak $3\times 3$-as négyzetekkel. Egy $5\times 6$-os téglalapot le lehet fedni az 1. ábrán látható módon. Egy $5\times 6k$-s téglalapot is le lehet fedni úgy, hogy $k$ db $5\times 6$-os téglalapra vágjuk, és ezeket már le tudjuk fedni. Egy $\left(2k+1\right)\times 6n$-es téglalapot pedig úgy fedünk le $\left(2k+1>5\right)$, hogy a széléről leválasztunk egy $5\times 6n$-es téglalapot. Ezt le tudjuk fedni, és maradt egy $\left(2k+1-5\right)\times 6n=\left(2k-4\right)\times 6n$-es téglalap, amit már le tudunk fedni csak $2\times 2$-es négyzetekkel.

1. ábra

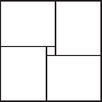2. ábra

 

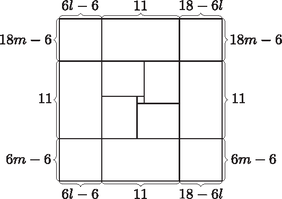3. ábra