Feladat:	B.4439	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Győrfi Mónika
Füzet:	2013/április, 224 - 225. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Ellipszis, mint mértani hely, Mértani közép, Ellipszis egyenlete
Hivatkozás(ok):	Feladatok: 2012/március: B.4439

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Megoldás. Vegyünk fel egy derékszögű koordinátarendszert úgy, hogy az origó egybeessen a $B$ ponttal, az $x$ tengely átmenjen $C$-n és válasszuk úgy az egységet, hogy $C=\left(1;0\right)$ legyen. Az $ABC$ háromszög $A$-hoz tartozó magasságának talppontja legyen $T$. Az $A$ pont pontosan akkor tartozik a keresett mértani helyhez, ha nincs rajta a $BC$ egyenesen és $\begin{array}{c}{\displaystyle AT=\sqrt[]{\left(BC+AC\right)\left(BC-AC\right)}\mathrm{,}}\end{array}$ azaz $\begin{array}{c}{\displaystyle A{T}^2=B{C}^2-A{C}^2}\end{array}$ teljesül. Vizsgáljuk meg, hogy az $A=\left(x;y\right)$ pont mikor tesz eleget a feltételeknek. A $T$ pont koordinátái $\left(x;0\right)$, ezért két pont távolságának ismert képlete alapján feltételünk $\begin{array}{c}{\displaystyle y^2=1-\left({\left(x-1\right)}^2+y^2\right)}\end{array}$ alakban írható. Ezt rendezve kapjuk, hogy $\begin{array}{c}{\displaystyle \frac{{\left(x-1\right)}^2}{1^2}+\frac{y^2}{(\frac{1}{\sqrt[]{2}}){}^2}=\mathrm{1,}}\end{array}$ ami egy olyan ellipszis egyenlete, amelynek nagytengelye $2a=2\cdot 1=2$, kistengelye $2b=2\cdot \frac{1}{\sqrt[]{2}}=\sqrt[]{2}$ hosszú, középpontja pedig az $\left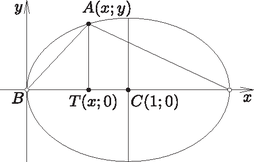(1;0\right)=C$ pont.     Tehát a keresett $A$ pontok mértani helye az az ellipszis, amelynek középpontja $C$, nagytengelyének egyik végpontja $B$, kistengelyének hossza pedig $\sqrt[]{2}BC$, kivéve a nagytengelyének végpontjait.