Feladat:	B.4402	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Bogáromi Dávid ,  Zahemszky Péter
Füzet:	2013/március, 156 - 157. oldal		PDF  |  MathML
Témakör(ök):	Körök, Számsorok, Mértani sorozat, Feladat
Hivatkozás(ok):	Feladatok: 2011/december: B.4402

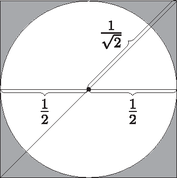
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. A külső nagy négyzet területe 1, a beleírt fehér kör sugara 1/2, ezért a legkülső sötét tartomány területe $1-\pi /4$. A következő négyzet átlója éppen a legnagyobb kör átmérője, vagyis 1, ezért az oldala $1/\sqrt[]{2}$-szerese, területe tehát ${\left(1/\sqrt[]{2}\right)}^2=1/2$-szerese a nagy négyzetének. Ugyanez az aránya a második és az első fehér kör területének is, ezért a második sötét rész területe az első sötét rész területének szintén a fele.     Hasonlósági megfontolásból ugyanezt a hányadost kapjuk, bármelyik sötét tartomány területét is osztjuk el a belülről közvetlenül mellette elhelyezkedő következő sötét tartományéval. A sötét részek területei tehát egy olyan mértani sorozatot alkotnak, amelynek első tagja $1-\pi /4$, hányadosa pedig $1/2$. A végtelen mértani sor összegképlete szerint tehát a sötét részek területének összege $\begin{array}{c}{\displaystyle T=\left(1-\frac{\pi }{4}\right)\cdot \frac{1}{1-\frac{1}{2}}=2-\frac{\pi }{2}\approx 0\mathrm{,}4292.}\end{array}$     II. megoldás. Jelöljük $T$-vel a keresett összeget. A legnagyobb fehér kör sugara 1/2, ezért a legkülső sötét tartomány területe $1-\pi /4$. Ahogy az első megoldásban láttuk, az első és a második négyzet oldalának aránya   $1/\sqrt[]{2}$. Ezért a legnagyobb fehér körön belüli sötét részeket megkapjuk, ha az egész ábrát $1/\sqrt[]{2}$-szeresére kicsinyítjük a középpontjából. Eközben a területek a hasonlóság arányának négyzetével arányosan változnak, azaz $1/2$-szeresükre csökkennek. Tehát $\begin{array}{c}{\displaystyle T=\left(1-\frac{\pi }{4}\right)+\frac{T}{2}\mathrm{.}}\end{array}$ Ebből pedig kapjuk, hogy a sötét részek területének összege $T=2-\pi /2$.