Feladat:	C.1116	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Gema Barnabás
Füzet:	2013/március, 151. oldal		PDF  |  MathML
Témakör(ök):	C gyakorlat, Terület, felszín, Középvonal, Négyszögek geometriája
Hivatkozás(ok):	Feladatok: 2012/március: C.1116

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.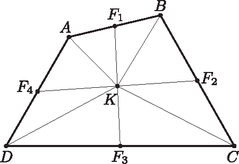   Megoldás. Először bizonyítsuk be, hogy egy konvex négyszöget a két középvonala olyan négyszögekre oszt, melyek közül a két-két szemközti területének összege egyenlő. Tekintsünk egy konvex négyszöget és húzzuk be a középvonalait, valamint a középvonalak metszéspontját a csúcsokkal összekötő szakaszokat.     Az $F_3$ pont a $DC$ szakasz felezőpontja, ezért $D{F}_3=F_{3}C$. A $D{F}_{3}K$ és $F_{3}CK$ háromszögek $K$ csúccsal szemközti oldalai egy egyenesre esnek és egyenlő hosszúak, és $K$ csúcsuk egybeesik (ezért a magasságuk egyenlő), így területük egyenlő. Ugyanez elmondható a $D{F}_{4}K$ és az $F_{4}KA$; az $AK{F}_1$ és az $F_{1}KB$, valamint az $F_{2}KB$ és az $F_{2}KC$ háromszögekről is. Így a következőket kapjuk: $T_{D{F}_{3}K}=T_{F_{3}CK}$, $T_{D{F}_{4}K}=T_{F_{4}KA}$, $T_{F_{1}KB}=T_{AK{F}_1}$, $T_{F_{2}KB}=T_{F_{2}KC}$. Összeadva:   ${\displaystyle \begin{array}{cc}\hfill {\displaystyle T_{D{F}_{3}K}+T_{D{F}_{4}K}+T_{F_{1}KB}+T_{F_{2}KB}}& {\displaystyle =T_{F_{3}CK}+T_{F_{4}KA}+T_{AK{F}_1}+T_{F_{2}KC}\mathrm{,}}\hfill \\ \hfill {\displaystyle T_{D{F}_{3}K{F}_4}+T_{K{F}_{1}B{F}_2}}& {\displaystyle =T_{F_{4}A{F}_{1}K}+T_{K{F}_{2}C{F}_3}\mathrm{,}}\hfill \end{array}}$ és ezt akartuk belátni. 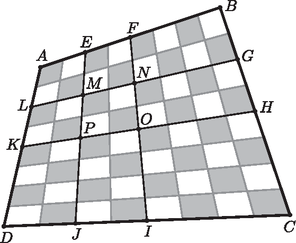    Most tekintsük a teljes sakktáblát. Ismeretes, hogy a konvex négyszögek középvonalai (az ábrán $FI$ és $KH$) felezik egymást. Vagyis az $O$ pont az $FI$ és a $KH$ szakasznak is felezőpontja. Tekintsük az $AFID$ négyszöget. Ennek $KO$ az egyik, $EJ$ pedig a másik középvonala. Mivel a középvonalak felezik egymást, a $P$ pont a $KO$ és az $EJ$ szakasznak is felezőpontja. Hasonló okokból az $N$ pont az $FO$ és az $LG$ szakaszok közös felezőpontja. Ebből pedig következik, hogy az $AFOK$ négyszögben az $M$ pont lesz az $LN$ és a $PE$ szakaszok felezőpontja, hiszen azok a négyszög középvonalai. Hasonló gondolatmenetek egymás utáni alkalmazásával megkapjuk, hogy az összes belső osztópont nyolcadolópont. Ez pedig azt jelenti, hogy például az $AFOK$ négyszögben a $2\times 2$-es sakktáblácskák is a középvonalaik mentén lettek felosztva, tehát a felosztásukkor keletkezett szemközti negyedeik, azaz a fehér és fekete negyedek területének összege egyenlő. Mivel a nagy sakktábla 16 ilyen kis táblácskából épül fel és ezekben a fekete és fehér négyszögek területe megegyezik, azért ez igaz a nagy sakktáblára is. Ezzel az állítást bebizonyítottuk.