Kezdőlap


Feladat:	B.4406	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Bősze Zsuzsanna , Di Giovanni Márk , Fehér Zsombor , Forrás Bence , Győrfi Mónika , Janzer Barnabás , Janzer Olivér , Jávorszky Natasa , Maga Balázs , Mester Márton , Nagy Róbert , Nagy-György Pál , Strenner Péter , Szabó Attila , Szabó Barnabás , Szilágyi Krisztina , Tossenberger Tamás , Viharos Andor , Zilahi Tamás
Füzet:	2013/február, 87 - 89. oldal		PDF \| MathML
Témakör(ök):	Egyenes, Egyenesek egyenlete, Feladat
Hivatkozás(ok):	Feladatok: 2011/december: B.4406

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.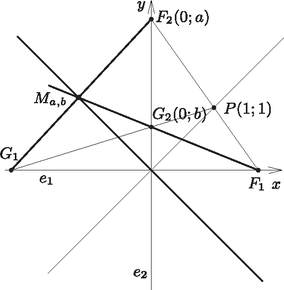

I. megoldás. Vegyünk fel egy derékszögű koordinátarendszert úgy, hogy annak

x

tengelye az

e_{1}

, az

y

tengelye az

e_{2}

egyenes legyen, az egységet pedig válasszuk úgy, hogy a

P

pont mindkét koordinátája 1 legyen. Ha

F_{2} = (0; a)

, ahol

a \neq 1

, akkor az

f

egyenes egyenlete

Y = (1 - a) X + a

, vagyis az

F_{1}

pont koordinátái

(\frac{a}{a - 1}; 0)

. Hasonlóképpen ha

G_{2} = (0; b)

, akkor a

g

egyenes egyenlete

Y = (1 - b) X + b

, a

G_{1}

pont koordinátái pedig

(\frac{b}{b - 1}; 0)

, ahol

b \neq 1

. Továbbá

a \neq b

is teljesül, mert

f

és

g

különböző egyenesek.

1. ábra

a

és

b

valamelyike 0, akkor az

F_{1} G_{2} \cap F_{2} G_{1}

metszéspont az origó. Ha

a \neq 0 \neq b

, akkor az

F_{1} G_{2}

és

F_{2} G_{1}

egyenesek egyenlete a tengelymetszeteikből egyszerűen felírható.

\begin{matrix} F_{1} G_{2} & : \frac{X}{\frac{a}{a - 1}} + \frac{Y}{b} = 1, azaz Y = \frac{b (1 - a)}{a} X + b, \\ F_{2} G_{1} & : \frac{X}{\frac{b}{b - 1}} + \frac{Y}{a} = 1, azaz Y = \frac{a (1 - b)}{b} X + a . \end{matrix}

\frac{b (1 - a)}{a} = \frac{a (1 - b)}{b}

, azaz

a + b = a b

, akkor a két egyenes párhuzamos. Ha

a + b \neq a b

, akkor létezik

M_{a, b} = (x_{0}; y_{0})

metszéspontjuk, és az egyenletrendszert megoldva kapjuk, hogy

\begin{matrix} x_{o} = \frac{a b}{a b - (a + b)} és y_{0} = \frac{- a b}{a b - (a + b)} = - x_{0}, \end{matrix}

ami azt jelenti, hogy

M_{a, b}

mindig rajta van az

Y = - X

egyenletű egyenesen, ami az

e_{1}

és

e_{2}

egyenesek másik szögfelezője.
Megmutatjuk, hogy az

Y = - X

egyenes minden pontja előáll

M_{a, b}

alakban. Az origóról már láttuk, hogy a mértani helyhez tartozik. Ezért elegendő azt meggondolnunk, hogy

a

és

b

megfelelő választásával

\frac{1}{x_{0}} = 1 - \frac{1}{a} - \frac{1}{b}

még az

a, b \neq 0,1

a \neq b

feltételek mellett is tetszőleges értéket felvehet, ami nyilvánvaló. A keresett mértani hely tehát az

e_{1}

és

e_{2}

egyenesek két szögfelezője közül a

P

pontot nem tartalmazó teljes szögfelező egyenes.

II. megoldás. Megmutatjuk, hogy a keresett mértani hely az

e_{1}

és

e_{2}

egyenesek másik szögfelezője.
Jelöljük

r

-rel az

e_{1}

és

e_{2}

egyenesek

P

pontot tartalmazó szögfelezőjét,

s

-sel pedig a két egyenes másik szögfelezőjét. Legyen

h

F_{2}

ponton átmenő

e_{1}

-gyel párhuzamos egyenes, továbbá legyen

O = e_{1} \cap e_{2}

Q = F_{1} G_{2} \cap F_{2} G_{1}

R = r \cap h

és

S = s \cap h

. Az

e_{1}

e_{2}

f

és

g

egyenesek lehetséges helyzetétől függően az

O

pont az

F_{1} G_{1}

és

F_{2} G_{2}

szakaszok közül egyiknek sem (2. ábra), pontosan egynek (3. ábra), vagy mindkettőnek (4. ábra) belső pontja. Következő állításaink mindhárom esetben érvényesek.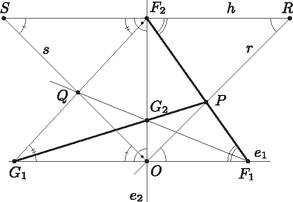

2. ábra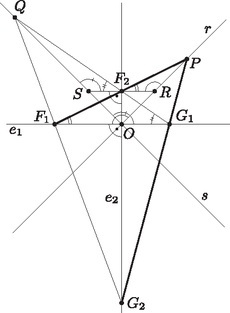

3. ábra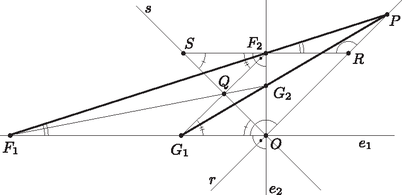

4. ábra

Mivel

h

és

e_{1}

párhuzamosak, a

P O F_{1}

és a

P R F_{2}

háromszögek, valamint a

Q O G_{1}

és a

Q S F_{2}

háromszögek is hasonlóak, mert megfelelő szögeik megegyeznek. Tehát a háromszögek megfelelő oldalainak aránya is egyenlő, azaz

\begin{matrix} \frac{F_{1} O}{P F_{1}} = \frac{F_{2} R}{F_{2} P} és \frac{G_{1} Q}{O G_{1}} = \frac{Q F_{2}}{F_{2} S} . \end{matrix}

(1)

Alkalmazzuk az

F_{1} G_{1} F_{2}

háromszögre és a

G_{2}

pontra Ceva tételének általánosítását. Mivel az

F_{1} Q

G_{1} P

és

F_{2} O

egyenesek mindegyike átmegy

G_{2}

-n, ezért

\begin{matrix} \frac{F_{1} O}{O G_{1}} \cdot \frac{G_{1} Q}{Q F_{2}} \cdot \frac{F_{2} P}{P F_{1}} = 1, azaz \frac{F_{1} O}{P F_{1}} \cdot \frac{G_{1} Q}{O G_{1}} \cdot \frac{F_{2} P}{Q F_{2}} = 1, \end{matrix}

amiből felhasználva az (1) egyenlőségeket, kapjuk, hogy

F_{2} R = F_{2} S

. Ez viszont azt jelenti, hogy az

O F_{2} R

és

O F_{2} S

háromszögek egybevágóak, mert megegyezik két-két oldaluk és az azok által bezárt szög (hiszen a

h

egyenes definíciója miatt

O F_{2} R ∢ = O F_{2} S ∢ = 90^{\circ}

.) Vagyis

F_{2} O Q ∢ = F_{2} O P ∢ = 45^{\circ}

, tehát

Q

rajta van az

s

egyenesen.
Megmutatjuk, hogy az

s

egyenes tetszőleges

T

pontja előáll

F_{1} G_{2} \cap F_{2} G_{1}

alakban megfelelően választott

f^{T}

és

g^{T}

egyenesek esetén. Először legyen

f^{T}

egy rögzített,

P

-n átmenő,

e_{i}

-t

F_{i}

-ben metsző egyenes,

G_{1}^{T} = F_{2} T \cap e_{1}

és

G_{2}^{T} = P G_{1}^{T} \cap e_{2}

. Ekkor a

P

-n átmenő

G_{1}^{T} G_{2}^{T}

egyenest választva

g^{T}

-nek, az

F_{1} G_{2} \cap F_{2} G_{1}

pont éppen

T

lesz. Ez az előállítás nem működik, ha

T F_{2}

és

e_{1}

párhuzamosak, valamint akkor sem, ha

T = f \cap s

. Ezt a két pontot úgy tudjuk előállítani

F_{1} G_{2} \cap F_{2} G_{1}

alakban, ha megváltoztatjuk az elsőnek felvett

f^{T}

egyenest. Ezzel elérhetjük, hogy az új egyeneshez tartozó két ,,rossz'' pont különbözzön az első egyeneshez tartozó rossz pontoktól.