Feladat: B.4437 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Szabó Bence 
Füzet: 2013/december, 538 - 539. oldal  PDF  |  MathML 
Témakör(ök): Feladat, Síkgeometriai szerkesztések, Háromszög nevezetes körei
Hivatkozás(ok):Feladatok: 2012/március: B.4437

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

 
Megoldás. Jelölje a szerkesztendő háromszög csúcsait és szögeit a szokásos módon A, B, C, illetve α, β, γ, a körülírt kör legyen k, középpontja K, a beírt kör középpontja O, a hozzáírt körök középpontjai pedig OA, OB és OC. Először megmutatjuk, hogy OAOBOC olyan hegyesszögű háromszög, amelynek talpponti háromszöge ABC, Feuerbach-köre pedig k (1. ábra, ezeket az állításokat a B. 4428. feladat megoldása1 során is beláttuk).
Tudjuk, hogy a beírt kör középpontja a három belső, a hozzáírt körök középpontjai pedig két külső és egy belső szögfelező metszéspontjai. A háromszög bármely csúcsához tartozó külső és belső szögfelezők merőlegesek egymásra, ezért AOA⊥OBOC, BOB⊥OAOC és COC⊥OBOA. Tehát az AOA, BOB és COC szakaszok az OAOBOC háromszög magasságszakaszai, azaz az A, B és C pontok e háromszög magasságvonalainak talppontjai, vagyis a rajtuk átmenő kör (ami egyúttal az ABC háromszög körülírt köre) az OAOBOC háromszög Feuerbach-köre. A hozzáírt körök középpontjainak szimmetrikus szerepe miatt az OAOBOC háromszög hegyesszögű voltának belátásához elegendő megmutatnunk, hogy 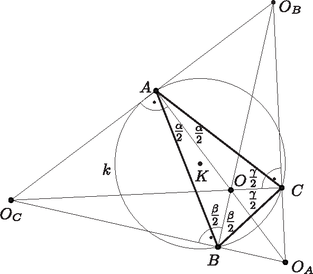OBOCOA∢<90∘. Mivel
ABOC∢=OBBOC∢-OBBA∢=90∘-OBA∢=90∘-β2,
és ugyanígy kapjuk, hogy BAOC∢=90∘-α2, azért
OBOCOA∢=AOCB∢=180∘-(ABOC∢+BAOC∢)==180∘-((90∘-β2)+(90∘-α2))=α+β2<α+β+γ2=90∘.


1.ábra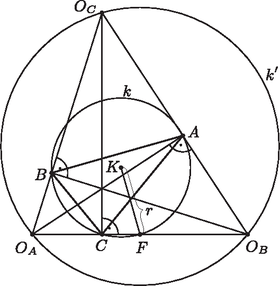

 


2.ábra

Ezek után felhasználva, hogy bármely háromszög Feuerbach-körének sugara éppen fele a háromszög köré írható kör sugarának, a szerkesztés már egyszerűen elvégezhető. Feltehetjük, hogy a hozzáírt körök középpontjai közül OA és OB adott.
Először megszerkesztjük az OAOB szakasz F felezőpontját, majd a K középpontú KF=r sugarú kört, ami megegyezik k-val. Ezek után megszerkesztjük az OAOBOC háromszög köré írható k' kört, tudván hogy ez áthalad az OA és OB pontokon, sugara pedig kétszerese a k kör sugarának (vagyis k' középpontja az OA, illetve OB középpontú 2r sugarú körök metszéspontja, sugara pedig 2r). A szerkesztendő háromszög C csúcsa a k kör és az OAOB szakasz F-től különböző metszéspontjaként adódik (vagy egybeesik F-fel, ha k érinti a szakaszt). A C-ben az OAOB egyenesre állított, a K-t tartalmazó félsíkba mutató merőleges félegyenes és k' metszéspontjaként megkapjuk az OC pontot. Végül az OA-ból OBOC-re, illetve OB-ből OAOC-re állított merőlegesek talppontjai adják az A, illetve B pontokat (2. ábra).
Az így szerkesztett ABC háromszög megfelel a feltételeknek, mert nyilván az OAOBOC háromszög talpponti háromszöge, azaz hozzáírt köreinek középpontjai rendre OA, OB és OC, körülírt köre pedig a K középpontú k kör.
A feladatnak legfeljebb egy megoldása van. Akkor kapunk megoldást, ha a szerkesztés minden lépését el tudjuk végezni, azaz ha a következő feltételek teljesülnek:
‐ A K pont nem esik az OAOB egyenesre, mert az OAOBOC háromszög belső pontja kell, hogy legyen.
‐ A K pontnak az OAOB szakaszra eső merőleges vetülete közelebb van az F ponthoz, mint az OA és OB pontok bármelyikéhez, ez ugyanis annak szükséges és elégséges feltétele, hogy a k körnek az OAOB egyenessel alkotott második metszéspontja (vagy érintési pontja) az OAOB szakasz belsejébe essen.
‐ A KF szakasz kétszerese hosszabb az OAOB szakasz felénél. Ez a szükséges és elégséges feltétele annak, hogy az OAOBOC háromszög hegyesszögű legyen.
1KöMaL, 2013/2., 94. o.