Kezdőlap


Feladat:	B.4359	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Baráti László , Bogár Blanka , Damásdi Gábor , Máthé László , Strenner Péter , Szabó Attila , Viharos Andor
Füzet:	2011/december, 539 - 541. oldal		PDF \| MathML
Témakör(ök):	Szabályos tetraéder, Szögfüggvények a térben, Feladat
Hivatkozás(ok):	Feladatok: 2011/április: B.4359

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ha az egymással párhuzamos $S_{1}$ és $S_{2}$ síkokat valamely $T$ sík az $e_{1}$ és $e_{2}$ egyenesekben metszi, akkor $e_{1}$ és $e_{2}$ párhuzamosak (1. ábra). Ugyanis egyrészt benne vannak a $T$ síkban, másrészt nem lehet közös pontjuk. Ha ugyanis valamely $P$ pont mindkét egyenesen rajta lenne, akkor $P$ az $S_{1}$ és $S_{2}$ síkok közös pontja lenne, ami ellentmond a két sík párhuzamosságának. Mivel egymással párhuzamos egyenesek bármely rögzített egyenessel egyenlő szögeket zárnak be, elegendő a $tg^{2} φ_{1} + tg^{2} φ_{2} + tg^{2} φ_{3}$ kifejezés értékeit abban az esetben meghatároznunk, ha a lapra merőleges sík átmegy a tetraéder negyedik csúcsán.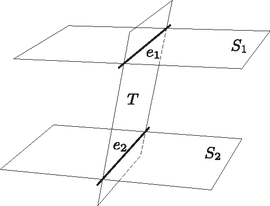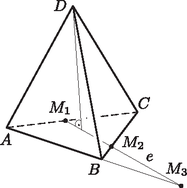

1. ábra

2. ábra

Feltehetjük tehát, hogy az

A B C D

szabályos tetraéder

A B C

lapsíkjára merőleges, azt az

e

egyenesben metsző

T

sík átmegy a tetraéder

D

csúcsán. Ekkor

T

átmegy az

A B C

lap

S

súlypontján is, mert a

D S

egyenes merőleges az

A B C

síkra. Jelölje

M_{1}

M_{2}

és

M_{3}

e

egyenes és az

A B C

háromszög oldalegyeneseinek metszéspontját (2. ábra). Ekkor

\begin{matrix} tg^{2} φ_{1} + tg^{2} φ_{2} + tg^{2} φ_{3} = \frac{D S^{2}}{S M_{1}^{2}} + \frac{D S^{2}}{S M_{2}^{2}} + \frac{D S^{2}}{S M_{3}^{2}}, \end{matrix}

mert a

D S M_{i}

háromszögek

S

-nél lévő szöge derékszög. Az

e

egyenes az

A B C

háromszög egyik oldalával párhuzamos is lehet. Ebben az esetben valamelyik

M_{i}

pont nem jön létre. Összefüggésünk azonban ekkor is érvényes, ha a párhuzamos egyenesek szögét szokás szerint

0^{\circ}

-nak tekintjük, az

\frac{1}{S M_{i}}

értékét pedig 0-nak.
Mivel a keresett kifejezés értéke
nyilván független a tetraéder élhosszától, feltehetjük, hogy az élek hossza 6. Ekkor

A S = \frac{6 \sqrt[]{3}}{3} = 2 \sqrt[]{3}

, tehát
Pitagorasz tétele szerint

D S^{2} = A D^{2} - A S^{2} = 24

. Ha bevezetjük az

a_{i} = S M_{i}

(i = 1,2,3)

jelölést, akkor tehát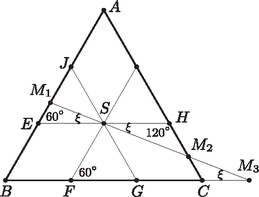

\begin{matrix} tg^{2} φ_{1} + tg^{2} φ_{2} + tg^{2} φ_{3} = 24 (\frac{1}{a_{1}^{2}} + \frac{1}{a_{2}^{2}} + \frac{1}{a_{3}^{2}}) . \end{matrix}

Vagyis elegendő az

a_{i}

szakaszok reciprokainak négyzetösszegét meghatároznunk. Ezzel feladatunkat visszavezettük egy síkbeli problémára.

3. ábra

Megmutatjuk, hogy a vizsgált négyzetösszeg értéke állandó. Rajzoljuk meg az

A B C

háromszög oldalaival párhuzamos,

S

-en átmenő egyeneseket. Ezek

A B C

-t három rombuszra és három kis szabályos háromszögre osztják (3. ábra). Ha

e

egybeesik a három párhuzamos valamelyikével, akkor az

\frac{1}{a_{i}}

értékek közül
az egyik 0, a másik kettő értéke pedig

\frac{1}{2}

. Tehát ekkor

\begin{matrix} \frac{1}{a_{1}^{2}} + \frac{1}{a_{2}^{2}} + \frac{1}{a_{3}^{2}} = \frac{1}{4} + \frac{1}{4} = \frac{1}{2} . \end{matrix}

e

A B C

háromszög egyik oldalával sem párhuzamos, akkor a három kis szabályos háromszög közül pontosan az egyiknek az

S

-sel szemközti oldalát metszi annak belső pontjában. A 3. ábra jelöléseit használva a szimmetria miatt feltehetjük, hogy ez a

J E S

kis háromszög, továbbá

M_{1}

J E

szakasz belső pontja és

S M_{2} \leq S M_{3}

. Ekkor

S E = S F = S H = 2

M_{1} E S ∢ = S F M_{3} ∢ = 60^{\circ}

és

S H M_{2} ∢ = 120^{\circ}

. Legyen

S M_{3} F ∢ = ξ

. Ekkor az egyállású és a váltószögek egyenlősége miatt

M_{1} S E ∢ = H S M_{2} ∢ = ξ

, továbbá

S M_{1} E ∢ = 120^{\circ} - ξ

és

S M_{2} H ∢ = 60^{\circ} - ξ

, mert bármely háromszögben a szögek összege

180^{\circ}

. A szinusztételt alkalmazva az

E S M_{1}

háromszögben, kapjuk, hogy

\begin{matrix} \frac{S E}{S M_{1}} = \frac{sin (120^{\circ} - ξ)}{sin 60^{\circ}}, azaz \frac{1}{a_{1}^{2}} = {(\frac{sin (120^{\circ} - ξ)}{2 sin 60^{\circ}})}^{2} = \frac{sin^{2} (120^{\circ} - ξ)}{3} . \end{matrix}

Ha pedig a

H S M_{2}

és

F S M_{3}

háromszögekben írjuk fel a szinusztételt, akkor ugyanígy kapjuk, hogy

\begin{matrix} \frac{1}{a_{2}^{2}} = \frac{sin^{2} (60^{\circ} - ξ)}{3} és \frac{1}{a_{3}^{2}} = \frac{sin^{2} ξ}{3} . \end{matrix}

Tehát felhasználva a

sin α = sin (180^{\circ} - α)

azonosságot, majd az addíciós képleteket alkalmazva

\begin{matrix} 3 (\frac{1}{a_{1}^{2}} + \frac{1}{a_{2}^{2}} + \frac{1}{a_{3}^{2}}) & = sin^{2} (ξ + 60^{\circ}) + sin^{2} (60^{\circ} - ξ) + sin^{2} ξ = \\ = sin^{2} ξ + {(\frac{1}{2} sin ξ + \frac{\sqrt[]{3}}{2} cos ξ)}^{2} + {(\frac{\sqrt[]{3}}{2} cos ξ - \frac{1}{2} sin ξ)}^{2} = \\ = \frac{3}{2} sin^{2} ξ + \frac{3}{2} cos^{2} ξ = \frac{3}{2} . \end{matrix}

Vagyis az

a_{i}

szakaszok reciprokainak négyzetösszege ekkor is

\frac{1}{2}

.
Ezért a

tg^{2} φ_{1} + tg^{2} φ_{2} + tg^{2} φ_{3}

kifejezés értéke, a metsző sík helyzetétől függetlenül, mindig

24 \cdot \frac{1}{2} = 12

lesz.