Kezdőlap


Feladat:	B.4350	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Ágoston Péter , Homonnay Bálint , Strenner Péter , Szabó Attila , Viharos Andor
Füzet:	2011/december, 537 - 539. oldal		PDF \| MathML
Témakör(ök):	Tetraéderek, Feladat, Ellenpélda, mint megoldási módszer a matematikában
Hivatkozás(ok):	Feladatok: 2011/március: B.4350

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Megmutatjuk, hogy a feltételből nem következik a tetraéder szabályossága. Egy konkrét ellenpélda helyett azt látjuk be, hogy a feladatban szereplő egyenlőtlenség minden egyenlő oldalú tetraéderre tejesül. Egy tetraédert egyenlő oldalúnak nevezünk, ha lapjai egybevágó háromszögek. Ilyen tetraédert alkot bármely téglatest két szemközti lapján lévő két nem párhuzamos lapátlójának négy végpontja (1. ábra). (Az egyenlő oldalú tetraéderekről részletes leírás található Reiman I.: Fejezetek az elemi geometriából című középiskolai tankönyvében. Ott megtalálható annak bizonyítása is, hogy minden egyenlő oldalú tetraéder valamely téglatestből származik az előzőekben leírt módon.)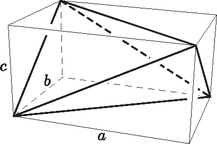

1. ábra

Ha a téglatest egy csúcsában találkozó éleinek hossza

a

b

és

c

, akkor a tetraéder minden lapja olyan háromszög, melynek oldalai Pitagorasz tétele szerint

\sqrt[]{a^{2} + b^{2}}

\sqrt[]{b^{2} + c^{2}}

és

\sqrt[]{a^{2} + c^{2}}

. Ebből azonnal adódik, hogy a tetraéder pontosan akkor szabályos, ha a téglatest kocka.
Először belátunk egy téglatestekre vonatkozó egyenlőtlenséget.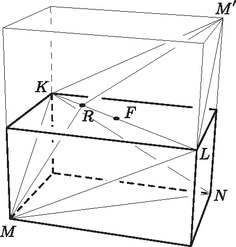

Segédtétel. Legyen

K L

és

M N

valamely

T

téglatest két szemközti lapján lévő két nem párhuzamos lapátlója. Ekkor a

K L

szakasz tetszőleges

R

belső pontja esetén fennáll az

\begin{matrix} R M + R N < K M + K N \end{matrix}

egyenlőtlenség.

2. ábra

Bizonyítás. Tükrözzük

T

-t a

K L

átló

F

felezőpontjára (2. ábra). Az

M

pont tükörképét jelölje

M'

. Mivel

K

tükörképe

L

, azért

K M

és

L M'

párhuzamosak és egyenlők. Tehát a

K M L M'

négyszög parallelogramma. Ezért

K M' = M L = K N

és

L M' = K M = L N

, vagyis a

K L M'

és

K L N

háromszögek egybevágóak. Ez azt jelenti, hogy

R M' = R N

, ezért elegendő belátnunk az

\begin{matrix} R M + R M' < K M + K N = K M + K M' \end{matrix}

(1)

egyenlőtlenséget.
A szimmetria miatt feltehetjük, hogy a

K M L M'

parallelogrammában

R

K M M'

háromszög pontja. Ha az

R

pont egybeesik

F

-fel, akkor (1) a háromszög-egyenlőtlenség miatt teljesül. Ha pedig

R

K M M'

háromszög belső pontja (3. ábra), akkor a B. 4325. feladat

a)

részének eredményét alkalmazva erre a háromszögre kapjuk (1)-et.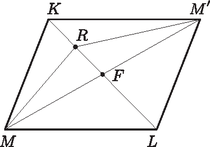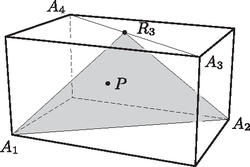

3. ábra

4. ábra

Térjünk vissza az eredeti feladatra. Legyen az

A_{1} A_{2} A_{3} A_{4}

egyenlő oldalú tetraéder éleinek hosszai

A_{1} A_{2} = A_{3} A_{4} = e

A_{1} A_{3} = A_{2} A_{4} = f

és

A_{1} A_{4} = A_{2} A_{3} = g

. A tetraéder tetszőleges

P

belső pontjára az 1, 2, 3 számok bármely

i

j

k

sorrendje esetén legyen az

A_{i} A_{j} P

sík és az

A_{4} A_{k}

él döféspontja

R_{k}

.
Mivel

P

A_{i} A_{j} R_{k}

háromszög belső pontja (4. ábra), ismét a B. 4325. feladat

a)

részének értelmében

P A_{i} + P A_{j} < R_{k} A_{i} + R_{k} A_{j}

. Viszont segédtételünk szerint

R_{k} A_{i} + R_{k} A_{j} < A_{4} A_{i} + A_{4} A_{j}

, tehát

\begin{matrix} P A_{i} + P A_{j} < A_{4} A_{i} + A_{4} A_{j} . \end{matrix}

Ezt az egyenlőtlenséget mindhárom

i

j

pár esetén felírva, majd összeadva az egyenlőtlenségeket, kapjuk, hogy

\begin{matrix} 2 (P A_{1} + P A_{2} + P A_{3}) < 2 (A_{4} A_{1} + A_{4} A_{2} + A_{4} A_{3}) = 2 (e + f + g) . \end{matrix}

Vagyis

\begin{matrix} P A_{1} + P A_{2} + P A_{3} < e + f + g, \end{matrix}

amiből szimmetria okokból már látszik, hogy a tetraéderre teljesül a feladat szövegében megfogalmazott feltételrendszer.

Megjegyzés. A feladatban szereplő egyenlőtlenség más tetraéderekben is fennáll. A megoldók többsége egy-egy konkrét tetraéderben mutatta meg, hosszadalmas számolással, hogy teljesül az egyenlőtlenség. Legtöbben olyan szabályos háromszög alapú egyenes gúlák esetét számolták ki, melyek oldalélének hossza nem sokkal tér el az alapélétől.