Feladat: B.4339 Korcsoport: 18- Nehézségi fok: nehéz
Füzet: 2011/december, 535 - 536. oldal  PDF  |  MathML 
Témakör(ök): Feladat, Térgeometriai bizonyítások, Tetraéderek, Gömb és részei
Hivatkozás(ok):Feladatok: 2011/február: B.4339

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az állítás igaz. Ennek bizonyításához először két segédtételt látunk be.

 
1. Bármely ABC háromszög tetszőleges P belső pontja esetén fennáll az
AP<max{AB,AC}
egyenlőtlenség. Azaz a háromszög belső pontját valamely csúccsal összekötő szakasz rövidebb, mint a háromszög adott csúcsból induló hosszabbik oldala.
 

Bizonyítás. Legyen az AP és BC egyenesek metszéspontja T (1. ábra). Ekkor AP<AT, és mivel T a BC szakasz belső pontja, azért az ATC és ATB szögek összege 180∘, tehát a két szög közül legalább az egyik legalább 90∘. Ekkor viszont az ATC vagy a BTC háromszögben ez a szög a legnagyobb. Mivel bármely háromszögben nagyobb szöggel szemben nagyobb oldal van, ez azt jelenti, hogy AB és AC szakaszok közül valamelyik biztosan nagyobb, mint AT.
 
 
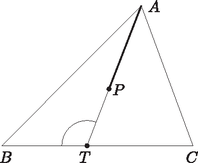1. ábra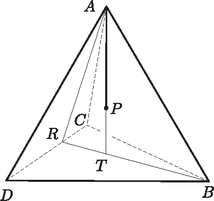
 
 
2. ábra
 

 
2. Bármely ABCD tetraéder tetszőleges P belső pontja esetén fennáll az
AP<max{AB,AC,AD}
egyenlőtlenség. Azaz a tetraéder belső pontját valamely csúccsal összekötő szakasz rövidebb, mint a tetraéder adott csúcsból induló leghosszabb éle.
 
Bizonyítás. Legyen az AP egyenes és a BCD sík döféspontja T. Ekkor AP<AT és T a BCD háromszög belső pontja. Ezért a BT egyenes is valamely R belső pontban metszi a tetraéder CD élét (2. ábra). Az 1. állítást először az ABR, majd pedig az ACD háromszögre alkalmazva kapjuk, hogy
AT<max{AB,AR}<max{AB,max{AC,AD}}=max{AB,AC,AD},
ami éppen a bizonyítandó állítás.
 
Eredeti feladatunk a 2. állítást felhasználva már könnyen megoldható. Jelölje a az ABCD szabályos tetraéder élhosszát. Ekkor tetszőleges P belső pont esetén AP<max{AB,AC,AD}=a, és ugyanígy kapjuk azt is, hogy BP<a és CP<a. Vagyis
PA+PB+PC<3a=DA+DB+DC,
ami éppen a bizonyítandó egyenlőtlenség.
 
Megjegyzés. A konvex halmazok tulajdonságait felhasználva a 2. állítást egyszerűbben is bizonyíthatjuk: Rajzoljuk meg az A középpontú r=max{AB,AC,AD} sugarú G gömböt. A tetraéder másik három csúcsa vagy G felületére illeszkedik, vagy pedig a belsejében van. Tehát a gömbtest, mely egy konvex alakzat, tartalmazza a csúcsok konvex burkát is, ami a teljes tetraéder. Ezért a tetraéder minden belső pontja egyúttal a gömbnek is belső pontja. Vagyis AP<r.