Kezdőlap


Feladat:	B.4335	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Kovács Márton
Füzet:	2011/december, 532 - 534. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Szinusztétel alkalmazása, Pont körre vonatkozó hatványa, Középponti és kerületi szögek, Feladat
Hivatkozás(ok):	Feladatok: 2011/február: B.4335

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az ábra jelölései alapján a $B C$ egyenes felezi az $A_{1} A_{2}$ szakaszt az $E$ pontban, mivel az $E$ pontnak mindkét körre vonatkozó hatványa: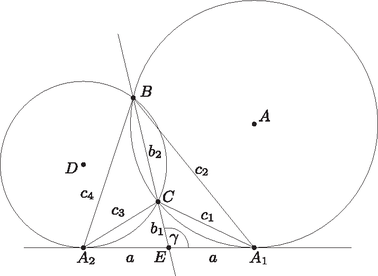

\begin{matrix} E C \cdot E B = A_{1} E^{2} = A_{2} E^{2} = a^{2} . \end{matrix}

Használjuk a következő jelöléseket:

\begin{matrix} E C = b_{1}, E B = b_{2}, A_{1} C = c_{1}, A_{1} B = c_{2}, A_{2} C = c_{3}, A_{2} B = c_{4} . \end{matrix}

Írjuk fel a koszinusztételt az

A_{1} C E

A_{1} B E

A_{2} C E

A_{2} B E

háromszögekre:

\begin{matrix} c_{1}^{2} & = a^{2} + b_{1}^{2} - 2 a b_{1} cos γ, \\ c_{2}^{2} & = a^{2} + b_{2}^{2} - 2 a b_{2} cos γ, \\ c_{3}^{2} & = a^{2} + b_{1}^{2} - 2 a b_{1} cos (180^{\circ} - γ) = a^{2} + b_{1}^{2} + 2 a b_{1} cos γ, \\ c_{4}^{2} & = a^{2} + b_{2}^{2} - 2 a b_{2} cos (180^{\circ} - γ) = a^{2} + b_{2}^{2} + 2 a b_{2} cos γ . \end{matrix}

A bizonyítandó állítás az új jelölésekkel:

\frac{c_{2}}{c_{1}} = \frac{c_{4}}{c_{3}}

.
Emeljük négyzetre mindkét oldalt:

\frac{c_{2}^{2}}{c_{1}^{2}} = \frac{c_{4}^{2}}{c_{3}^{2}}

, majd helyettesítsük be a koszinusz tétellel kapott kifejezéseket:

\begin{matrix} \frac{a^{2} + b_{2}^{2} - 2 a b_{2} cos γ}{a^{2} + b_{1}^{2} - 2 a b_{1} cos γ} = \frac{a^{2} + b_{2}^{2} + 2 a b_{2} cos γ}{a^{2} + b_{1}^{2} + 2 a b_{1} cos γ} . \end{matrix}

A nevezőkkel beszorozva és rendezve a következő egyenlethez jutunk:

\begin{matrix} 4 a^{3} b_{1} cos γ + 4 a b_{1} b_{2}^{2} cos γ - 4 a^{3} b_{2} cos γ - 4 a b_{1}^{2} b_{2} cos γ = 0. \end{matrix}

Ezután oszthatunk

4 a

-val, mivel az nem lehet 0 (különben csak egy érintési pont lenne, és nem lennének metszéspontok). A

cos γ

-val is tudunk osztani, mivel

cos γ = 0

esetén

γ = 90^{\circ}

, ami azt jelenti, hogy

A_{1} B A_{2}

és

A_{1} C A_{2}

egyenlő szárú háromszögek, és az egyenlő szárak miatt nyilvánvalóan teljesül az állítás. Így azt kell belátnunk, hogy

\begin{matrix} a^{2} b_{1} + b_{1} b_{2}^{2} - a^{2} b_{2} - b_{1}^{2} b_{2} = 0. \end{matrix}

Szorzattá alakítva:

\begin{matrix} a^{2} (b_{1} - b_{2}) - b_{1} b_{2} (b_{1} - b_{2}) = (a^{2} - b_{1} b_{2}) (b_{1} - b_{2}) = 0. \end{matrix}

Itt

a^{2} - b_{1} b_{2} = 0

mindig teljesül, mivel

a^{2} = b_{1} b_{2}

igaz az

E

pont körre vonatkozó hatványa miatt. Tehát, mivel ekvivalens átalakításokat hajtottunk végre, a feladat állítása igaz.