Kezdőlap


Feladat:	B.4474	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Szeidl Balázs Vince
Füzet:	2013/november, 477. oldal		PDF \| MathML
Témakör(ök):	Feladat, Síkgeometriai bizonyítások, Háromszögek hasonlósága, Pitagorasz-tétel alkalmazásai
Hivatkozás(ok):	Feladatok: 2012/október: B.4474

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Pitagorasz tételét a $K B L$ és az $A D M$ , valamint az $A B L$ és az $M D N$ derékszögű háromszögekre felírva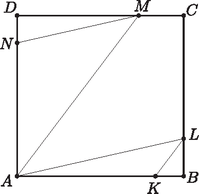

\begin{matrix} K L^{2} + A M^{2} = (K B^{2} + B L^{2}) + (D A^{2} + D M^{2}), \end{matrix}

és

\begin{matrix} L A^{2} + M N^{2} = (A B^{2} + B L^{2}) + (N D^{2} + D M^{2}) . \end{matrix}

Mivel

A B = D A

, a bizonyítandó egyenlőség ezzel a

K B^{2} = N D^{2}

, vagyis

K B = N D

alakot ölti. Ezt pedig a következőképpen láthatjuk be. Az

A L K

és

L A M

szögek egyenlősége miatt

L K

párhuzamos

A M

-mel, ezért az

A D M

és

L B K

derékszögű háromszögek hasonlóak. Ugyanígy,

L A

és

M N

párhuzamosak lévén hasonlóak egymáshoz az

M D N

és

A B L

derékszögű háromszögek is. E hasonlóságok következtében

\begin{matrix} K B : B L = D M : D A, azaz K B = \frac{B L \cdot D M}{D A}, \end{matrix}

illetve

\begin{matrix} N D : D M = B L : A B, azaz N D = \frac{B L \cdot D M}{A B} . \end{matrix}

Ismét felhasználva, hogy

A B = D A

, innen valóban

K B = N D

.
Megjegyzés. A feladatban csupán a

K L A

L A M

és

A M N

szögek egyenlőségének van szerepe, közös értéküknek viszont nincs.