Kezdőlap


Feladat:	B.4457	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Lelkes János
Füzet:	2013/november, 475 - 476. oldal		PDF \| MathML
Témakör(ök):	Feladat, Síkgeometriai számítások trigonometriával, Konstruktív megoldási módszer, Koszinusztétel alkalmazása
Hivatkozás(ok):	Feladatok: 2012/május: B.4457

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.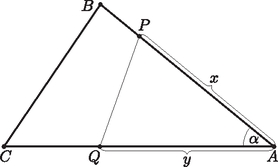

Megoldás. Először általában adunk alsó becslést egy háromszög területét felező szakasz hosszára. Ha a

P Q

szakasz felezi az

A B C

háromszög területét, akkor az eredeti háromszög két része közül legalább az egyik egy háromszög (akkor lesz mindkét rész háromszög, ha a

P Q

szakasz tartalmazza az

A B C

háromszög valamelyik csúcsát). Mivel alsó becslést adunk, feltehetjük, hogy

P

és

Q

A B C

háromszög két oldalára esik, az oldalak szimmetrikus szerepe miatt pedig azt is, hogy

P

A B

Q

pedig az

A C

szakasz

A

-tól különböző pontja. Legyen

A P = x

és

A Q = y

(1. ábra).

1. ábra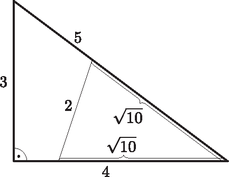

2. ábra

Ha az

A B C

háromszög területét

T

, az

A

csúcsánál lévő szöget pedig

α

jelöli, akkor az

A P Q

háromszög területe

\begin{matrix} \frac{T}{2} = \frac{A P \cdot A Q \cdot sin α}{2} = \frac{x y sin α}{2} . \end{matrix}

Az ebből adódó

x y = \frac{T}{sin α}

összefüggést, valamint a koszinusztételt és a négyzetes és a mértani közepek közti egyenlőtlenséget felhasználva kapjuk, hogy

\begin{matrix} P Q^{2} = x^{2} + y^{2} - 2 x y cos α \geq 2 x y (1 - cos α) = 2 T \frac{1 - cos α}{sin α} . \end{matrix}

(1)

Mivel

1 - cos α = 2 sin^{2} \frac{α}{2}

és

sin α = 2 sin \frac{α}{2} \cdot cos \frac{α}{2}

, azért

\begin{matrix} P Q^{2} \geq 2 T \frac{1 - cos α}{sin α} = 2 T tg \frac{α}{2}, \end{matrix}

ahol egyenlőség akkor és csak akkor áll fenn, ha

x = y = \sqrt[]{A B \cdot \frac{A C}{2}}

.
Térjünk vissza az eredeti feladatunkra. Hegyesszögek esetén a tangens függvény szigorúan monoton nő, ezért a legrövidebb területfelező szakaszt akkor kapjuk, ha a

3

4

és

5

oldalakkal rendelkező háromszög legkisebb szögét közrefogó két oldalon, azaz a

4

és

5

hosszú oldalakon

vesszük fel a

P

és

Q

pontokat úgy, hogy

A P = A Q = \sqrt[]{5 \cdot \frac{4}{2}} = \sqrt[]{10}

teljesüljön.

\sqrt[]{10} < 4

miatt megtehető (2. ábra). Ekkor

cos α = \frac{4}{5}

, ezért az (1) egyenlőségből kapjuk, hogy

\begin{matrix} P Q^{2} = 10 + 10 - 20 \cdot \frac{4}{5} = 4. \end{matrix}

Tehát a háromszög területét felező szakaszok közül a legrövidebbnek a hossza 2.