Feladat:	B.4444	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Leitereg András
Füzet:	2013/november, 469 - 471. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Síkgeometriai bizonyítások, Húrnégyszögek, Középponti és kerületi szögek
Hivatkozás(ok):	Feladatok: 2012/április: B.4444

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Megoldás. Megmutatjuk, hogy $L$ is és $M$ is rajta van az $AFB$ körön. Ehhez elegendő belátnunk, hogy $\begin{array}{c}{\displaystyle ALB\sphericalangle =AMB\sphericalangle ={180}^{\circ }-AFB\sphericalangle \mathrm{.}}\end{array}$ (1) Jelöljük az $ABCD$ négyzet oldalának hosszát $a$-val. Az elforgatások miatt az $ADE$ és $CBG$ háromszögek olyan egybevágó egyenlőszárú háromszögek, amelyek szárainak hossza $a$, szárszögük $\alpha$, s így alapon fekvő szögeik nagysága ${90}^{\circ }-\frac{\alpha }{2}$. Ezért az $AFB$ háromszög $A$-nál és $B$-nél lévő külső szögeinek összege   $\begin{array}{c}{\displaystyle \left({90}^{\circ }+\alpha \right)+\left({90}^{\circ }+{90}^{\circ }-\frac{\alpha }{2}\right)={270}^{\circ }+\frac{\alpha }{2}\mathrm{.}}\end{array}$   Tudjuk, hogy egy háromszög bármely külső szöge megegyezik a nem mellette lévő két belső szög összegével, ezért ‐ felhasználva, hogy a háromszögben a szögek összege 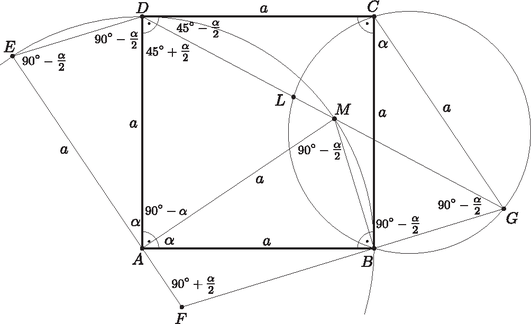${180}^{\circ }$ ‐ kapjuk, hogy   $\begin{array}{c}{\displaystyle AFB\sphericalangle =\left({270}^{\circ }+\frac{\alpha }{2}\right)-{180}^{\circ }={90}^{\circ }+\frac{\alpha }{2}\mathrm{.}}\end{array}$   Mivel $DC=CB=CG=a$ és $DCG\sphericalangle ={90}^{\circ }+\alpha$, a $DCG$ egyenlőszárú háromszögben $CDG\sphericalangle =CGD\sphericalangle ={45}^{\circ }-\frac{\alpha }{2}$. Ebből kapjuk, hogy   $\begin{array}{c}{\displaystyle ADM\sphericalangle =ADC\sphericalangle -CDG\sphericalangle ={45}^{\circ }+\frac{\alpha }{2}\mathrm{.}}\end{array}$   Mivel $AE=AD=AB=a$, azért a $BDE$ kör középpontja $A$, és így $AM=AD=a$ is teljesül (1. ábra).     1. ábra   Az $ADM$ és $AMB$ háromszögek tehát egyenlőszárúak, ezért 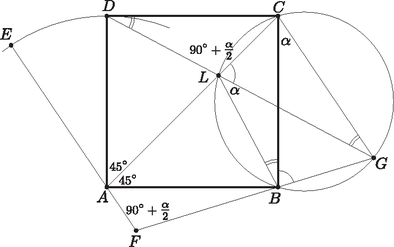$DAM\sphericalangle ={180}^{\circ }-2ADM\sphericalangle ={90}^{\circ }-\alpha$, s mivel $MAB\sphericalangle ={90}^{\circ }-DAM\sphericalangle =\alpha$, azért $\begin{array}{c}{\displaystyle AMB\sphericalangle =\frac{{180}^{\circ }-MAB\sphericalangle }{2}={90}^{\circ }-\frac{\alpha }{2}={180}^{\circ }-AFB\sphericalangle \mathrm{.}}\end{array}$ Tehát $M$ rajta van az $AFB$ körön.     2. ábra   Mivel $\alpha$ hegyesszög, a $G$ és $L$ pontok a $BC$ egyenes különböző oldalaira esnek (2. ábra). Így a $GC$ húrhoz tartozó kerületi szögek egyenlősége miatt $CLG\sphericalangle =CBG\sphericalangle ={90}^{\circ }-\frac{\alpha }{2}$, amiből kapjuk, hogy $CLD\sphericalangle ={180}^{\circ }-CLG\sphericalangle ={90}^{\circ }+\frac{\alpha }{2}$. A $GB$ húrhoz tartozó kerületi szögek egyenlősége miatt pedig $GLB\sphericalangle =GCB\sphericalangle =\alpha$, ezért $\begin{array}{c}{\displaystyle CLB\sphericalangle =CLG\sphericalangle +GLB\sphericalangle =\left({90}^{\circ }-\frac{\alpha }{2}\right)+\alpha ={90}^{\circ }+\frac{\alpha }{2}=CLD\sphericalangle \mathrm{.}}\end{array}$ Végül pedig a $CL$ húrhoz tartozó kerületi szögek egyenlősége miatt $LBC\sphericalangle =LGC\sphericalangle =DGC\sphericalangle =GDC\sphericalangle =LDC\sphericalangle$. Tehát az $LBC$ és $LDC$ háromszögek egybevágóak, mert közös az $LC$ oldaluk és két-két megfelelő szögük egyenlő. Ezért $LCB\sphericalangle =LCD\sphericalangle$, vagyis $L$ rajta van az $ABCD$ négyzet $AC$ átlóján. Ezért $\begin{array}{c}{\displaystyle ALB\sphericalangle ={180}^{\circ }-CLB\sphericalangle ={90}^{\circ }-\frac{\alpha }{2}={180}^{\circ }-AFB\sphericalangle \mathrm{,}}\end{array}$ vagyis teljesül rá az (1) egyenlőség. Ezzel megmutattuk, hogy mind az öt pont egy körön van.