Feladat: B.4327 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Janzer Barnabás 
Füzet: 2011/december, 528 - 529. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek szerkesztése, Súlyvonal, Apollóniusz-kör, Feladat
Hivatkozás(ok):Feladatok: 2011/január: B.4327

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tekintsük a feladatot megoldottnak. Az ABC egyenlőszárú háromszög BC és AC szárainak felezőpontja legyen F, illetve G, a háromszög súlypontja pedig S (1. ábra). Felhasználva, hogy a súlypont harmadolja a súlyvonalakat, valamint azt, hogy egyenlőszárú háromszögben a szárakhoz tartozó súlyvonalak is egyenlők, kapjuk, hogy

GS=FS=SA2=AF3=BG3.

Ezek alapján ha adott az AF súlyvonal, továbbá a CAF szög, akkor a szerkesztést a következő módon végezhetjük. Felvesszük az AF szakaszt és megszerkesztjük ennek F-hez közelebbi harmadolópontját, ami megegyezik S-sel. Ezután az AF félegyenessel az adott α szöget bezáró f félegyenest indítunk A-ból (erre két lehetőség van), ezen kell lennie a G és C pontoknak. Mivel G az S középpontú SF sugarú k körön is rajta van, f és k közös pontjaként megkapjuk G-t. Ezután a GS szakasz S-en túli meghosszabbítására GS kétszeresét felmérve kapjuk B-t. Végül az AG és BF egyenesek metszéspontja adja a háromszög C 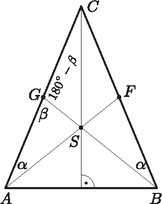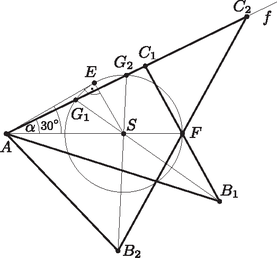csúcsát.
 
 
1. ábra
 
 
2. ábra
 

Az így szerkesztett háromszög szimmetrikus az AB szakasz felezőmerőlegesére, ezért egyenlőszárú. Az is nyilvánvaló, hogy CAF∢=CBG∢=α. Ha bevezetjük az AGS∢=β jelölést, akkor BGC∢=180∘-β, így a szinusztételt az AGS és a BGC háromszögekben felírva kapjuk, hogy
12=GSSA=sinαsinβ=sinαsin(180∘-β)=CGBC.
Ezért CG fele olyan hosszú, mint a háromszög szárai, vagyis G oldalfelezőpont. Akkor viszont a szimmetria miatt F is az, tehát AF valóban súlyvonala a szerkesztett ABC háromszögnek.
A megoldások száma k és f közös pontjainak számától függ. A szimmetria miatt a két félegyenes közül elég az egyiket tekintenünk. Ha az A pontból a k körhöz húzott egyik érintő érintési pontja E (2. ábra), akkor az AES derékszögű háromszögben sinEAS∢=ESSA=12, azaz az érintő az AF félegyenessel 30∘-os szöget zár be. Ezért α>30∘ esetén a feladatnak nincsen megoldása. Ha α=30∘, akkor egy megoldás van, ha pedig 0∘<α<30∘, akkor két különböző megoldást kapunk.