Kezdőlap


Feladat:	B.4499	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Györfi Mónika
Füzet:	2013/szeptember, 349 - 350. oldal		PDF \| MathML
Témakör(ök):	Feladat, Síkgeometriai bizonyítások, Körérintők, Pitagorasz-tétel alkalmazásai
Hivatkozás(ok):	Feladatok: 2012/december: B.4499

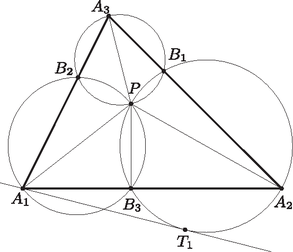
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Jelölje a $P A_{i}$ átmérőjű kört $k_{i}$ $(i = 1,2,3)$ . Legyenek a $P$ pontból az $A_{1} A_{2}$ , $A_{2} A_{3}$ , $A_{3} A_{1}$ oldalakra bocsátott merőlegesek talppontjai rendre $B_{3}$ , $B_{1}$ , $B_{2}$ az ábra szerint.
A megfelelő körök második metszéspontja minden esetben a $B_{i}$ pont. Igazoljuk ezt például a $B_{3}$ pontra: az $A_{1} P$ és $A_{2} P$ a $k_{1}$ , illetve $k_{2}$ körök átmérői; $B_{3}$ a $P$ -ből állított merőleges talppontja az $A_{1} A_{2}$ oldalon, így mindkét körnek pontja a Thálesz-tétel miatt.

Írjuk fel az

A_{1}

pont

k_{2}

körre vonatkozó hatványát kétféleképpen:

\begin{matrix} A_{1} T_{1}^{2} = A_{1} B_{3} \cdot A_{1} A_{2} . \end{matrix}

A többi körre is felírva ugyanezt látjuk, hogy

\begin{matrix} A_{2} T_{2}^{2} & = A_{2} B_{1} \cdot A_{2} A_{3}, \\ A_{3} T_{3}^{2} & = A_{3} B_{2} \cdot A_{3} A_{1} . \end{matrix}

Most írjuk fel a

P A_{1} B_{3}

, a

P A_{2} B_{1}

és a

P A_{3} B_{2}

háromszögekre a Pitagorasz-tételt:

\begin{matrix} P A_{1}^{2} & = P B_{3}^{2} + A_{1} B_{3}^{2}, & (1) \\ P A_{2}^{2} & = P B_{1}^{2} + A_{2} B_{1}^{2}, & (2) \\ P A_{3}^{2} & = P B_{2}^{2} + A_{3} B_{2}^{2} . & (3) \end{matrix}

Ezután pedig a

P B_{3} A_{2}

háromszögre írjuk fel a Pitagorasz-tételt, de kicsit másképpen, az előző adatokra támaszkodva:

\begin{matrix} P B_{3}^{2} + {(A_{1} A_{2} - A_{1} B_{3})}^{2} = P A_{2}^{2} . \end{matrix}

Ezt kifejtve látjuk, hogy a kétszeres szorzat a korábbiak alapján

2 \cdot A_{1} T_{1}^{2}

-re cserélhető.

\begin{matrix} P B_{3}^{2} + A_{1} A_{2}^{2} - 2 \cdot A_{1} A_{2} \cdot A_{1} B_{3} + A_{1} B_{3}^{2} & = P A_{2}^{2}, \\ P B_{3}^{2} + A_{1} A_{2}^{2} - 2 \cdot A_{1} T_{1}^{2} + A_{1} B_{3}^{2} & = P A_{2}^{2} . & (4) \end{matrix}

Ugyanilyen módon kapjuk a

P B_{1} A_{3}

és

P B_{2} A_{1}

háromszögekre, hogy

\begin{matrix} P B_{1}^{2} + A_{2} A_{3}^{2} - 2 \cdot A_{2} T_{2}^{2} + A_{2} B_{1}^{2} & = P A_{3}^{2}, & (5) \\ P B_{2}^{2} + A_{3} A_{1}^{2} - 2 \cdot A_{3} T_{3}^{2} + A_{3} B_{2}^{2} & = P A_{1}^{2} . & (6) \end{matrix}

Most adjuk össze az (1)‐(6) egyenleteket:

\begin{matrix} P A_{1}^{2} + P A_{2}^{2} + P A_{3}^{2} + P B_{3}^{2} + A_{1} A_{2}^{2} - 2 \cdot A_{1} T_{1}^{2} + A_{1} B_{3}^{2} + P B_{1}^{2} + \\ + A_{2} A_{3}^{2} - 2 \cdot A_{2} T_{2}^{2} + A_{2} B_{1}^{2} + P B_{2}^{2} + A_{3} A_{1}^{2} - 2 \cdot A_{3} T_{3}^{2} + A_{3} B_{2}^{2} = \\ = P B_{3}^{2} + A_{1} B_{3}^{2} + P B_{1}^{2} + A_{2} B_{1}^{2} + P B_{2}^{2} + A_{3} B_{2}^{2} + P A_{2}^{2} + P A_{3}^{2} + P A_{1}^{2}, \end{matrix}

majd végezzük el a lehetséges egyszerűsítéseket:

\begin{matrix} A_{1} A_{2}^{2} + A_{2} A_{3}^{2} + A_{3} A_{1}^{2} = 2 (A_{1} T_{1}^{2} + A_{2} T_{2}^{2} + A_{3} T_{3}^{2}), \end{matrix}

ezzel éppen a bizonyítandó állítást kapjuk.