Feladat:	B.4387	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	2012/április, 223 - 224. oldal		PDF  |  MathML
Témakör(ök):	Húrsokszögek, Szögfüggvények, síkgeometriai számítások, Háromszög területe, Feladat
Hivatkozás(ok):	Feladatok: 2011/október: B.4387

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Legyen a hatszög köré írható $k$ kör középpontja $O$, sugarának hosszát pedig válasszuk $\sqrt[]{2}$-nek. Ekkor az ismert területképlet szerint ha $P$ és $R$ tetszőleges pontok $k$-n, akkor $\begin{array}{c}{\displaystyle T_{OPR}=\frac{OP\cdot OR}{2}\text{sin}POR\sphericalangle =\frac{\sqrt[]{2}\cdot \sqrt[]{2}}{2}\text{sin}POR\sphericalangle =\text{sin}POR\sphericalangle \mathrm{.}}\end{array}$ (1) Az $O$ pont a hatszög belsejében van, ellenkező esetben ugyanis a hatszög valamelyik oldala (feltehetjük, hogy $AB$) elválasztaná $O$-t a hatszög többi csúcsától (1. ábra). Ebből viszont következne, hogy a hatszög öt másik oldala mind rövidebb lenne, mint $AB$, vagyis nem teljesülhetne az $AB=BC$ egyenlőség. 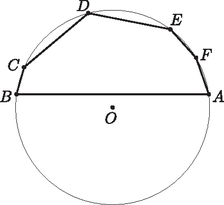  1. ábra     2. ábra   Jelölje $\alpha$, $\beta$ és $\gamma$ rendre a $k$ körben az $AB$, $CD$ és $EF$ húrokhoz tartozó középponti szögeket. Tudjuk, hogy egy körben egyenlő húrokhoz egyenlő középponti szögek tartoznak, ezért a $BC$, $DE$ és $FA$ húrokhoz tartozó középponti szögek is rendre $\alpha$, $\beta$ és $\gamma$ (2. ábra). S mivel $O$ a hatszög belső pontja, azért $\begin{array}{c}{\displaystyle 2\left(\alpha +\beta +\gamma \right)={360}^{\circ }\mathrm{,}\text{azaz}\alpha +\beta +\gamma ={180}^{\circ }\mathrm{.}}\end{array}$ Vagyis az (1) képlet alapján a hatszög területe ${\displaystyle \begin{array}{cc}\hfill {\displaystyle T_{ABCDEF}}& {\displaystyle =T_{OAB}+T_{OBC}+T_{OCD}+T_{ODE}+T_{OEF}+T_{OFA}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =2\left(\text{sin}\alpha +\text{sin}\beta +\text{sin}\gamma \right)\mathrm{.}}\hfill \end{array}}$ A $BDF$ háromszög területe pedig $\begin{array}{c}{\displaystyle T_{BDF}=T_{OBD}+T_{ODF}+T_{OFB}=\text{sin}\left(\alpha +\beta \right)+\text{sin}\left(\beta +\gamma \right)+\text{sin}\left(\gamma +\alpha \right)\mathrm{.}}\end{array}$ Viszont $\alpha +\beta +\gamma ={180}^{\circ }$ miatt a $\text{sin}x=\text{sin}\left({180}^{\circ }-x\right)$ összefüggés alapján kapjuk, hogy $\begin{array}{c}{\displaystyle \text{sin}\left(\alpha +\beta \right)+\text{sin}\left(\beta +\gamma \right)+\text{sin}\left(\gamma +\alpha \right)=\text{sin}\gamma +\text{sin}\alpha +\text{sin}\beta \mathrm{,}}\end{array}$ tehát $T_{ABCDEF}=2T_{BDF}$, ami éppen a bizonyítandó állítás.   II. megoldás. Ismert, hogy ha egy hatszög köré kör írható, akkor a hatszög főátlói egy ponton mennek át. Ez Brianchon tételének speciális esete, a bizonyítás megtalálható pl. Hajós Gy.: Bevezetés a geometriába című könyvében, a 48.3. részben. Eszerint tehát az $AD$, $BE$ és $CF$ szakaszoknak van egy közös $K$ pontjuk (3. ábra). Ez a pont a $BDF$ háromszög belső pontja, mert a $BE$, $DA$ és $FC$ szakaszok rendre a $DBF$, $FDB$ és $BFD$ szögtartományokban vannak, közös pontjuk tehát e három szögtartomány metszetében, azaz a $BDF$ háromszögben helyezkedik el.   3. ábra   Megmutatjuk, hogy a $C$ pont $BD$ egyenesre vonatkozó tükörképe $K$. Mivel egy körben egyenlő húrokhoz egyenlő kerületi szögek tartoznak, az $AB=BC$ egyenlőségből $ADB\sphericalangle =CDB\sphericalangle$, a $CD=DE$ egyenlőségből pedig $CBD\sphericalangle =EBD\sphericalangle$ következik. Vagyis a tükrözés szögtartása miatt $C$-nek $BD$-re vonatkozó tükörképe rajta van a $DA$ és a $BE$ egyeneseken is. E két egyenes egyetlen közös pontja $K$, tehát csak ez lehet a $C$ pont $BD$ egyenesre vonatkozó tükörképe. Ekkor pedig a $BCD$ és a $BKD$ háromszögek egybevágóak. Ugyanígy láthatjuk be, hogy a $DEF$ háromszög egybevágó a $DKF$ háromszöggel, az $FAB$ pedig az $FKB$-vel. Ezek után feladatunk állításának belátása már egyszerű: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle T_{ABCDEF}}& {\displaystyle =T_{BDF}+T_{BCD}+T_{DEF}+T_{FAB}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =T_{BDF}+T_{BKD}+T_{DKF}+T_{FKB}=2T_{BDF}\mathrm{.}}\hfill \end{array}}$