|
| Feladat: |
B.4391 |
Korcsoport: 16-17 |
Nehézségi fok: nehéz |
| Megoldó(k): |
Ágoston Péter , Ágoston Tamás , Bingler Arnold , Fehér Zsombor , Gyarmati Máté , Havasi Márton , Herczeg József , Janzer Olivér , Kabos Eszter , Kaprinai Balázs , Mester Márton , Schulz Vera Magdolna , Strenner Péter , Tardos Jakab , Varnyú József , Viharos Andor |
| Füzet: |
2012/március,
154 - 156. oldal |
 PDF | PDF |  MathML MathML |
| Témakör(ök): |
Konvex sokszögek, Síkgeometriai bizonyítások, Síkgeometriai számítások trigonometriával, Feladat |
| Hivatkozás(ok): | Feladatok: 2011/október: B.4391 |
|
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megoldás. Legyen és jelölje az ötszög csúcsait , az csúccsal szemközti oldalt , az szakaszt tartalmazó egyenesen az csúcstól távol-
ságra lévő pontot pedig . Mivel minden szöge , az szakasz felezi az ötszög -nél lévő belső szögét. A magasságok különbözőségéből következik az oldalak
hosszának különbözősége. Ha ugyanis valamely csúcsban találkozó két oldal lenne egyenlő hosszú, akkor a szögek egyenlősége miatt az egyenes szimmetriatengelye lenne, ha pedig két nem szomszédos oldal lenne egyenlő hosszú, akkor annak az oldalnak a felezőmerőlegesére lenne szimmetrikus , amelynek a két egyenlő oldal mindegyikével van közös csúcsa (1. ábra). Tengelyesen szimmetrikus ötszög magasságai közt viszont vannak egyenlőek.
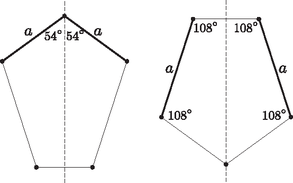 1. ábra
Először megmutatjuk, hogy bármelyik irányban számozzuk is a csúcsokat, az indexeket modulo 5 tekintve teljesülnek az | | (1) |
összefüggések. Legyen az pontból az egyenesre állított merőleges talppontja . Az ötszög minden szöge , ezért az ötszög konvex, amiből következik, hogy az szakasz belső pontja; ezért . Az derékszögű háromszögben az -nél lévő szög , (mert felezi az ötszög -nél lévő szögét), ezért az -nél lévő szög , s így (2. ábra). Mivel az szakasz egyenesre eső merőleges vetülete és , azért . Ezeket összeadva pedig adódik az (1) összefüggés első fele. A második részt ugyanígy bizonyíthatjuk, csak az csúcsból kell merőlegest állítanunk az szakaszra.
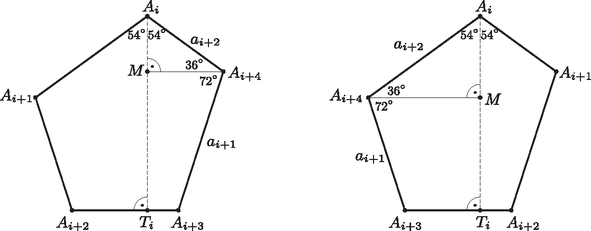 2. ábra
Az (1) összefüggések alapján viszont a magasságok közti egyenlőtlenségeket könnyen átírhatjuk az ötszög oldalaira vonatkozó egyenlőtlenségekké. Mivel
azért pontosan akkor teljesül, ha . Ugyanígy kapjuk, hogy
Összefoglalva tehát pontosan akkor teljesül, ha és .
Az oldalak nagyságrendjére vonatkozó két egyenlőség teljesülését pedig elérhetjük pl. a következő választással. Legyen a leghosszabb oldal és válasszuk az irányítást úgy, hogy a két szomszédja közül legyen a kisebb. Az másik szomszédja , ezért , az egyenlőtlenség pedig azért teljesül, mert a legnagyobb oldal. Tehát így a feltételeknek megfelelően számozzuk meg az oldalakat.
Strenner Péter
|
|
 PDF |
PDF |  MathML
MathML 
