Feladat:	B.4389	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Ágoston Péter ,  Ágoston Tamás ,  Barna István ,  Dinev Georgi ,  Fehér Zsombor ,  Gyarmati Máté ,  Győrfi Mónika ,  Havasi Márton ,  Homonnay Bálint ,  Janzer Olivér ,  Maga Balázs ,  Máthé László ,  Mester Márton ,  Ódor Gergely ,  Strenner Péter ,  Tossenberger Tamás
Füzet:	2012/március, 153 - 154. oldal		PDF  |  MathML
Témakör(ök):	Kör (és részhalmaza), mint mértani hely, Körérintők, Feladat
Hivatkozás(ok):	Feladatok: 2011/október: B.4389

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.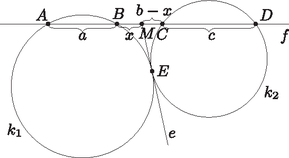   Megoldás. Legyenek $k_1$ és $k_2$ egymást az $E$ pontban érintő olyan körök, melyek közül $k_1$ átmegy az $A$ és $B$, $k_2$ pedig a $C$ és $D$ pontokon. Mivel az adott $f$ egyenesnek ekkor a körökkel csak az $AB$, illetve $CD$ szakaszok a metszetei, a pontok sorrendjéből következik, hogy a két kör kívülről érinti egymást. Ezért az $e$-vel jelölt $E$-beli közös érintőjük a $BC$ szakasz belsejében lévő $M$ pontban metszi az $f$ egyenest.     Megmutatjuk, hogy az $M$ pont nem függ a köröktől, az $A$, $B$, $C$ és $D$ pontok egyértelműen meghatározzák $M$ helyét, valamint az $ME$ szakasz hosszát. Legyen $AB=a$, $BC=b$, $CD=c$ és $BM=x$. Tudjuk, hogy külső pontból egy körhöz húzott két szelőszakasz szorzata megegyezik a pontból a körhöz húzott érintőszakasz hosszának négyzetével. Az $M$-ből $k_1$-hez és $k_2$-höz ugyanaz az $ME$ érintőszakasz húzható, ezért 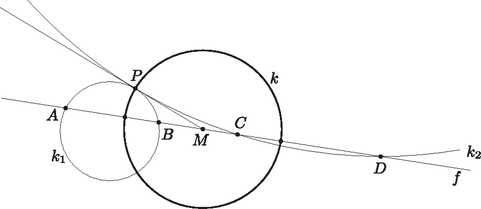$\begin{array}{c}{\displaystyle M{E}^2=MA\cdot MB=MC\cdot MD\mathrm{,}}\end{array}$ azaz $\begin{array}{c}{\displaystyle \left(a+x\right)x=\left(b-x\right)\left(b+c-x\right)\mathrm{.}}\end{array}$ Ebből kapjuk, hogy $\begin{array}{c}{\displaystyle x=\frac{b^2+bc}{a+2b+c}\mathrm{,}\text{és így}\frac{x}{b-x}=\frac{b+c}{a+b}\mathrm{,}}\end{array}$ továbbá $\begin{array}{c}{\displaystyle ME=\sqrt[]{\frac{b\left(b+c\right)\left(a+b\right)\left(a+b+c\right)}{{\left(a+2b+c\right)}^2}}\mathrm{.}}\end{array}$ Tehát az $M$ pont adott arányban osztja a $BC$ szakaszt, és az $ME$ távolság is állandó. Vagyis $E$ rajta van azon a $k$ körön, amelynek középpontja $\frac{b+c}{a+b}$ arányban osztja $BC$-t, sugara pedig $r=ME$.     Megmutatjuk, hogy a keresett mértani hely a $k$ kör, kivéve az $f$ egyenessel vett két metszéspontját. Ehhez már csak azt kell belátnunk, hogy ha $P$ a $k\setminus f$ halmaz tetszőleges pontja, akkor léteznek az $\left\{A\mathrm{,}B\mathrm{,}P\right\}$, illetve a $\left\{C\mathrm{,}D\mathrm{,}P\right\}$ ponthármasokon átmenő, egymást $P$-ben érintő körök. Mivel $P$ nincs rajta az $f$ egyenesen, egyértelműen léteznek az $\left\{A\mathrm{,}B\mathrm{,}P\right\}$, illetve a $\left\{C\mathrm{,}D\mathrm{,}P\right\}$ ponthármasokon átmenő $k_1$, illetve $k_2$ körök. Az $M{P}^2=MA\cdot MB$ egyenlőségből következik, hogy az $MP$ egyenes $P$-ben érinti a $k_1$ kört, az $M{P}^2=MC\cdot MD$ egyenlőségből pedig, hogy $P$-ben érinti a $k_2$ kört is. Vagyis a két kör $P$-beli érintőegyenese megegyezik, azaz a két kör érinti egymást $P$-ben. Ezzel állításunkat beláttuk.    Dinev Georgi