Feladat: B.4375 Korcsoport: 14-15 Nehézségi fok: könnyű
Füzet: 2012/március, 149 - 150. oldal  PDF  |  MathML 
Témakör(ök): Háromszög területe, Feladat, Síkgeometriai számítások trigonometria nélkül háromszögekben
Hivatkozás(ok):Feladatok: 2011/szeptember: B.4375

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.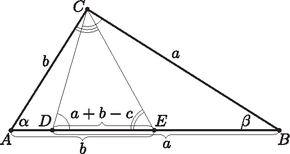

 
I. megoldás.
 
A háromszög területe ab2 és cm2 alakban is felírható, ezért 2ab=2cm. Ezt, valamint Pithagorasz tételét, továbbá a nyilvánvaló m2>0 egyenlőtlenséget felhasználva kapjuk, hogy
(a+b)2=a2+b2+2ab=c2+2cm<c2+2cm+m2=(c+m)2.
Mivel a négyzetgyökvonás a pozitív számok rendezését megtartja, ebből a+b<m+c következik.
 
 
II. megoldás. Jelöljük a háromszög csúcsait és szögeit a szokásos módon A, B, C-vel, illetve α, β, γ-val. Legyenek D és E az AB szakasz azon pontjai, melyekre BD=BC=a és AE=AC=b. Ekkor DE=a+b-c (1. ábra). Megmutatjuk, hogy m>DE.
 
 
1. ábra
 

Az AEC és BCD háromszögek egyenlőszárúak, ezért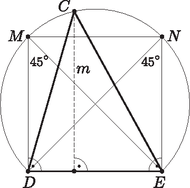
ACE∢=AEC∢=180∘-α2=90∘-α2ésBCD∢=BDC∢=180∘-β2=90∘-β2.
Tehát a CDE háromszög D-nél és E-nél lévő szögei hegyesszögek, C-nél lévő szöge pedig
DCE∢=ACE∢+BCD∢-ACB∢=90∘-α2+90∘-β2-90∘==90∘-α+β2=45∘.

 
 
2. ábra
 

Ezért C rajta van a DE szakasz fölé emelt 45∘-os k látóköríven. Jelölje a DE egyenesre D-ben, illetve E-ben állított merőlegesek és k metszéspontját M, illetve N (2. ábra). Ekkor DME∢=DNE∢=45∘, ezért DM=DE=EN, a DENM négyszög szimmetrikus a DE szakasz felezőmerőlegesére és a négyszög két szöge derékszög. Tehát DENM négyzet, k pedig e négyzet körülírt körének egy íve. Mivel a CDE háromszög hegyesszögű, C az M és N pontok közt helyezkedik el k-n. Vagyis C távolabb van a DE egyenestől, mint M és N. Ez azt jelenti, hogy m nagyobb, mint a DENM négyzet oldala, azaz m>a+b-c.
Tehát az m+c szakasz nagyobb, mint az a+b.