Kezdőlap


Feladat:	B.4321	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bogár Blanka , Damásdi Gábor , Dudás Zsolt , Énekes Péter , Fonyó Viktória , Lenger Dániel , Máthé László , Szabó Attila , Tekeli Tamás , Viharos Andor
Füzet:	2011/október, 412 - 413. oldal		PDF \| MathML
Témakör(ök):	Feladat, Trigonometrikus egyenlőtlenségek, Húrnégyszögek, Középponti és kerületi szögek
Hivatkozás(ok):	Feladatok: 2010/december: B.4321

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Vegyük fel az $A$ csúcsból kiinduló szögharmadolókat, metszéspontjuk az $a$ oldallal legyen $H_{1}$ és $H_{2}$ . Vizsgáljuk először az $A C H_{2}$ háromszöget. Szögei $γ$ , $\frac{α}{3}$ és $180^{\circ} - \frac{α}{3} - γ$ . A szinusztétel alapján:

\begin{matrix} \frac{b}{C H_{2}} = \frac{sin (180^{\circ} - \frac{α}{3} - γ)}{sin \frac{α}{3}} = \frac{sin (\frac{α}{3} + γ)}{sin \frac{α}{3}}, vagyis \frac{b}{sin (\frac{α}{3} + γ)} = \frac{C H_{2}}{sin \frac{α}{3}} . \end{matrix}

Hasonlóan az

A B H_{1}

háromszögből kapjuk, hogy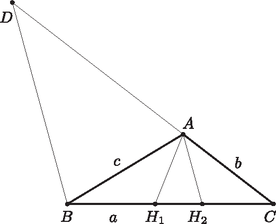

\begin{matrix} \frac{c}{B H_{1}} = \frac{sin (\frac{α}{3} + β)}{sin \frac{α}{3}} \Rightarrow \frac{c}{sin (\frac{α}{3} + β)} = \frac{B H_{1}}{sin \frac{α}{3}} . \end{matrix}

Ezeket a feladatban szereplő egyenlőtlenségbe helyettesítve ezt kapjuk:

\begin{matrix} \frac{C H_{2}}{sin \frac{α}{3}} + \frac{B H_{1}}{sin \frac{α}{3}} > \frac{2 a}{3 sin \frac{α}{3}}, \end{matrix}

illetve egyszerűsítve:

\begin{matrix} C H_{2} + B H_{1} > \frac{2}{3} a . \end{matrix}

(1)

Ha ezt belátjuk, beláttuk az állítást.
Húzzunk párhuzamost a

B

ponton keresztül

A H_{2}

-vel, ennek

A B

-vel való metszéspontja legyen

D

. Az

A B D

háromszög szögei ekkor

\frac{α}{3}

\frac{2 α}{3}

180^{\circ} - α

. A szinusztétel alapján:

\begin{matrix} \frac{A D}{c} = \frac{sin \frac{2 α}{3}}{sin \frac{α}{3}} = \frac{2 sin \frac{α}{3} cos \frac{α}{3}}{sin \frac{α}{3}} = 2 cos \frac{α}{3} . \end{matrix}

Tehát

A D = c \cdot 2 cos \frac{α}{3}

. A párhuzamos szelők tétele alapján:

\begin{matrix} \frac{C H_{2}}{a} = \frac{b}{b + A D} = \frac{b}{b + c \cdot 2 cos \frac{α}{3}} \Rightarrow C H_{2} = \frac{a b}{b + c \cdot 2 cos \frac{α}{3}} . \end{matrix}

Hasonló módon beláthatjuk, hogy

\begin{matrix} B H_{1} = \frac{a c}{c + b \cdot 2 cos \frac{α}{3}} . \end{matrix}

Ezek alapján:

\begin{matrix} C H_{2} + B H_{1} = \frac{a b}{b + c \cdot 2 cos \frac{α}{3}} + \frac{a c}{c + b \cdot 2 cos \frac{α}{3}} . \end{matrix}

Mivel

cos \frac{α}{3} < 1

, a nevezőket növelve:

\begin{matrix} C H_{2} + B H_{1} > \frac{a b}{b + c \cdot 2} + \frac{a c}{c + b \cdot 2} = a \cdot (\frac{b}{b + 2 c} + \frac{c}{c + 2 b}) . \end{matrix}

Tehát (1)-hez elegendő belátni, hogy

\frac{b}{b + 2 c} + \frac{c}{c + 2 b} \geq \frac{2}{3}

. Közös nevezőre hozva:

\begin{matrix} \frac{b c + 2 b^{2} + b c + 2 c^{2}}{b c + 2 b^{2} + 2 c^{2} + 4 b c} = \frac{2 b^{2} + 2 b c + 2 c^{2}}{2 b^{2} + 5 b c + 2 c^{2}} \geq \frac{2}{3} . \end{matrix}

Minden érték pozitív, így átszorozva

\begin{matrix} 6 b^{2} + 6 b c + 6 c^{2} & \geq 4 b^{2} + 10 b c + 4 c^{2}, azaz \\ 2 b^{2} - 4 b c + 2 c^{2} & \geq 0, \\ 2 {(b - c)}^{2} & \geq 0. \end{matrix}

Tehát az állítás igaz.