Kezdőlap


Feladat:	B.4292	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Herczeg József , Kecskés Boglárka
Füzet:	2011/október, 406 - 407. oldal		PDF \| MathML
Témakör(ök):	Feladat, Beírt kör, Húrnégyszögek, Középponti és kerületi szögek
Hivatkozás(ok):	Feladatok: 2010/október: B.4292

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A szögfelezők a háromszögbe írható kör $O$ középpontjában metszik egymást. A $D$ , $E$ és $F$ pontok mindegyikéből a $C O$ szakasz derékszögben látszik, tehát ezek a pontok mind rajta vannak a $C O$ szakasz $k$ Thalész-körén.

1. ábra

A B C

háromszög szögeit jelölje

2 α

2 β

és

2 γ

(1. ábra). Ekkor felhasználva, hogy bármely háromszög külső szöge megegyezik a nem mellette lévő két belső szög összegével kapjuk, hogy

\begin{matrix} E O C ∢ = α + γ és F O C ∢ = β + γ . \end{matrix}

Mivel

α + β + γ = 90^{\circ}

, ebből

\begin{matrix} E O F ∢ = (α + γ) + (β + γ) = 90^{\circ} + γ \end{matrix}

következik. Tehát a

k

körben az

E F

húrhoz tartozó egyik kerületi szög

90^{\circ} + γ

, így a hozzá tartozó másik kerületi szög

180^{\circ} - (90^{\circ} + γ) = 90^{\circ} - γ

.
A

C O D

háromszög

D

-nél lévő szöge derékszög, ezért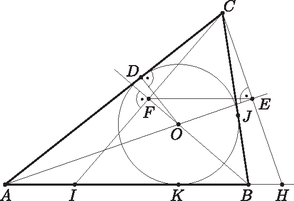

\begin{matrix} C O D ∢ = 90^{\circ} - D C O ∢ = 90^{\circ} - γ . \end{matrix}

Tehát a

k

körben a

C D

és

E F

húrhoz egyaránt

90^{\circ} - γ

nagyságú kerületi szög tartozik, ezért a két húr ugyanolyan hosszú.

II. megoldás. Legyen a beírt körnek az

A B

, illetve

B C

oldalon lévő érintési pontja

K

, illetve

J

, jelölje továbbá a

C E

és

C F

egyenesek

A B

egyenessel való metszéspontját

H

és

I

(2. ábra), az

A B C

háromszög oldalainak a hosszát pedig

a

b

és

c

2. ábra

H C A

háromszögben az

A

csúcshoz tartozó

A E

belső szögfelező merőleges a

H C

oldalra, ezért a háromszög egyenlőszárú,

H A = A C = b

. Ezért

A E

felezi a háromszög alapját, tehát

H E = E C

. Ugyanígy kapjuk, hogy az

I B C

háromszög is egyenlőszárú,

I B = B C = a

és

I F = F C

. A

H I C

háromszögben tehát

E F

középvonal, aminek hossza a megfelelő oldal hosszának fele, azaz

E F = H I / 2

. Mivel

H I = H A + B I - A B = b + a - c

, azért

E F = (a + b - c) / 2

.
Tudjuk, hogy egy körhöz bármely külső pontból két egyenlő hosszúságú érintőszakasz húzható, ezért

A D = A K

C D = C J

és

B K = B J

. Így

\begin{matrix} C D & = A C - A D = A C - A K = A C - (A B - B K) = A C - A B + B J = \\ = A C - A B + (B C - C J) = b - c + a - C D, \end{matrix}

amiből átrendezéssel kapjuk, hogy

C D = (a + b - c) / 2

.
Tehát

C D = E F

, ami épp a bizonyítandó állítás.