Feladat: 2009. évi Nemzetközi Matematika Diákolimpia 23. feladata Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Nagy János 
Füzet: 2011/október, 391 - 394. oldal  PDF  |  MathML 
Témakör(ök): Síkgeometriai bizonyítások, Tengelyes tükrözés, Inverzió, Körülírt kör, Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):Feladatok: 2011/szeptember: 2009. évi Nemzetközi Matematika Diákolimpia 23. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Nagy János megoldása. Legyenek az ℓb, ℓc és ℓa egyenesek által meghatározott háromszög csúcsai rendre A', B' és C'; és legyen az A'B'C' háromszög körülírt köre Γ', ekkor azt kell igazolnunk, hogy Γ' és Γ körök érintik egymást.
A Γ kör és az A'B'C' háromszög, illetve Γ' kör között csak gondolati kapcsolat van eddig, kell valami, ami fizikaivá teszi. Ehhez vegyük észre, hogy az A'B'C' háromszög beírt körének I középpontja rajta van a Γ körön és ráadásul az IA, IB, IC egyenesek átmennek rendre az A', B' és C' pontokon.

 
 

Ezt az állításunkat nem fogjuk bebizonyítani, mert nincs is rá szükség, elég ha tudjuk intuitívan, hogy ez igaz. Legyenek az ABC háromszög szögei α, β, γ, amik tehát hegyesszögek.
Most a következőt fogjuk belátni: Legyen A'B'C' egy háromszög, melynek szögei
180∘-2α,180∘-2βés180∘-2γ,
ennek körülírt köre k', beírt körének középpontja I, és k egy olyan kör, ami átmegy az I ponton, és érinti a k' kört. A k kör és az IA', IB', IC' egyenesek második metszéspontja A, B és C. Ekkor az AB egyenesre tükrözve az A'B' egyenest, a BC egyenesre tükrözve a B'C' egyenest és a CA egyenesre tükrözve a C'A' egyenest, ugyanazt az egyenest kapjuk, ami ráadásul érinti a k kört.
Egyrészt belátjuk ezt az állítást, másrészről megmutatjuk, hogy ebből következik a feladat állítása:
Először is ebben a helyzetben az ABC háromszög szögei α, β és γ, mert a k körben a kerületi szögek tétele miatt a háromszög szögei megegyeznek az A'B'C' háromszög szögfelezőinek egymással bezárt szögeivel, amik éppen α, β és γ.
Most tekintsük a fix A'B' egyenes AB egyenesre való tükörképét.
Ha a k kör helyzetét közben változtatjuk, akkor könnyen látható, hogy az AB egyenes minden irányt fel fog venni k összes helyzetét tekintve, mert minden irányhoz tudunk találni olyan kört, amely átmegy I-n, és akkor ezt hasonlósággal át tudjuk vinni olyanba, ami érinti a k' kört.
Így tehát az AB egyenes és a tükörkép szöge is tetszőleges lehet, az egyéb diszkussziós meggondolásokat most mellőzzük.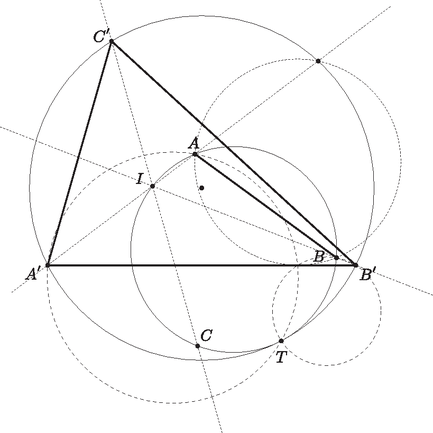
 
 

Van tehát olyan helyzete a k körnek, amelyre az A, B, C és a közös tükörképek érintési pontja a k körrel; e négy pont által meghatározott négyszög hasonló az eredeti feladatban levő ABCP négyszöghöz. De ekkor a hasonlóság az eredeti feladat két körét az itteni k és k' körökbe viszi, amik érintik egymást, tehát ekkor készen lennénk.
Most tehát igazoljuk az állításunkat. Az, hogy a tükörképek érintik a k kört, szimmetrikus állítások, így elég közülük az egyiket igazolni, mi az A'B' egyenes tükörképével tesszük ezt.
Ehelyett azt látjuk be, hogy ha az AB egyenesre tükrözzük a k kört, akkor az érinti az A'B' egyenest valamilyen X pontban, ami természetesen ekvivalens átfogalmazás.
Azt kell észrevenni még, hogy ez az X pont rajta lesz az A'AT háromszög, illetve a B'BT háromszög körülírt körén is.
Tehát megmutatjuk, hogy az A'AT háromszög, illetve a B'BT háromszög körülírt köre az A'B' egyenesen metszi egymást, utána pedig belátjuk, hogy ez az X metszéspont rajta van a tükrözött körön, sőt érintési pont is egyben.
Először is lássuk be, hogy az A'AT háromszög, illetve a B'BT háromszög körülírt köre az A'B' egyenesen metszi egymást, tegyük fel hogy az első kör metszéspontja az A'B' egyenessel X1, a másodiké pedig X2; azt akarjuk belátni, hogy X1=X2.
Ehhez az kell, hogy
TX1A'∢+TX2B'∢=180∘,
de
TX1A'∢+TX2B'∢=TAA'∢+TBB'∢=IAT∢+180∘-IBT∢=180∘,
ahol végig a kerületi szögek tételét használtuk.
Legyen tehát X=X1=X2, belátjuk, hogy X rajta van az AB-re tükrözött k körön; ehhez azt kell igazolnunk, hogy
AXB∢=180∘-ATB∢=180∘-AIB∢=180∘-γ,
de
AXB∢=180∘-AXA'∢-BXB'∢=180∘-ATA'∢-BTB'∢==180∘-γ-ATA'∢-BTB'∢+γ=180∘-γ.
Felhasználtuk, hogy A'TB'C' húrnégyszög.
Ezzel megkaptuk, hogy X rajta van a tükrözött körön is, még az kell, hogy érintési pont is egyben.
Ehhez invertáljuk az ábrát a T pontból, ekkor a képábrán A, A' és X képei egy egyenesen lesznek, és B, B' és X képei is egy egyenesen lesznek az inverzió szabályai szerint.
Ezen kívül AB képe párhuzamos lesz A'B' képével, mert az eredeti ábrán az ABT kör érinti az A'B'T kört, így tehát a képábrán az XAB és XA'B' háromszögek hasonlóak, tehát körülírt körük érintik egymást.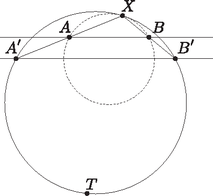

 
 

Ezeknek a köröknek az ősképei az AXB kör, illetve az A'B' egyenes, mert A', X és B' egy egyenesen vannak az eredeti ábrán, ezért az inverzió szögtartása miatt az A'B' egyenes az eredeti ábrán valóban érinti az AXB körülírt körét, vagyis a tükrözött kört.
Ezzel bebizonyítottuk, hogy ha az AB egyenesre tükrözzük az A'B' egyenest, akkor a kép érinti a k kört, és ugyanígy a többi csúcspárra is, már csak azt kéne belátni, hogy ez az érintési pont mind a három alkalommal ugyanaz lesz.
Legyen az A, B csúcspárra ez az érintési pont E1, a B, C csúcspárra pedig E2, ekkor a szimmetria miatt elég belátni hogy E1=E2, és akkor mindhárom érintési pontnak meg kell egyeznie.
Tehát tudjuk, hogy XAB∢=BXB'∢ az érintő szárú kerületi szögek tétele miatt, és akkor a bizonyítottak szerint E1AB∢=XAB∢=BXB'∢=BTB'∢.
Teljesen szimmetrikusan E2AB∢=E2CB∢=BTB'∢, abból pedig akkor az E1 és E2 pontnak meg kell egyezni, vagy tükrösnek kell lennie az AB egyenesre; de ezt mindegyik Ei, Ej párra elmondhatjuk a szimmetria miatt és akkor ez már csak tényleg úgy lehet, hogy ha az E1, E2, E3 pontok megegyeznek: ha közülük semelyik kettő nem egyezne meg, akkor a felező merőlegeseik egy ponton mennének át, de ez az AB, AC, BC oldalakra nyilván nem teljesül. Ha pedig kettő megegyezik, a harmadik meg más, akkor két felező merőleges teljesen megegyezne, ami megint csak nem teljesülhet két oldalra.
Így tehát igazoltuk az állításunkat, és ‐ mint azt korábban megmutattuk ‐ ezzel bizonyítottuk az eredeti feladat állítását is.