Feladat: B.4190 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Bodor Bertalan ,  Lovas Lia Izabella 
Füzet: 2012/február, 83 - 86. oldal  PDF  |  MathML 
Témakör(ök): Feladat, Vektorok, Tér parkettázás, Oszthatóság
Hivatkozás(ok):Feladatok: 2009/május: B.4190

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

 
I. megoldás. A kívánt kitöltés lehetséges. Azt fogjuk megmutatni, hogy egy két kockányi vastagságú térrész kitölthető a kívánt módon, méghozzá úgy, hogy sem alul, sem fölül nincsenek ,,kilógó'' részek. Ekkor ilyen két kockányi vastagságú térrészek egymásra helyezésével az egész tér kitölthető.
Minden ábránk felülnézeti lesz. Bevezetünk néhány jelölést:
 a két egymás feletti kocka közül már mindkettő kitöltött;
 csak az alsó kocka kitöltött;
 csak a felső kocka kitöltött.
Azokat a kockákat, ahol még sem az alsó, sem a felső kocka nincs kitöltve, nem jelöljük az ábrán.
Elhelyezzük az első testet: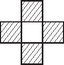  
A következő testet megfordítva rakjuk le mellé, tehát öt kocka a felső kockarétegben fog elhelyezkedni, egy pedig az alsóban. Az utóbbi egy kocka éppen az előző test két kockája közé kerül (ábránkon a felső és a jobboldali közé):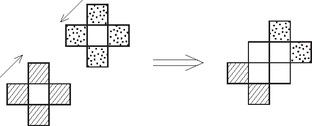
 
 

Gyártsunk további ilyen alakzatokat. Két ilyet egymásra csúsztatva: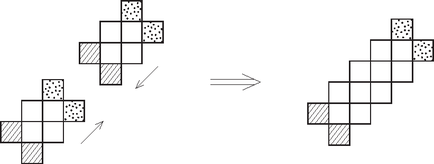
 
 

Végtelen sok ilyen alakzat összetolásával a következő végtelen ,,lépcsős alakzatot'' kapjuk: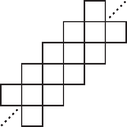
 
 

Toljunk össze két ilyen alakzatot: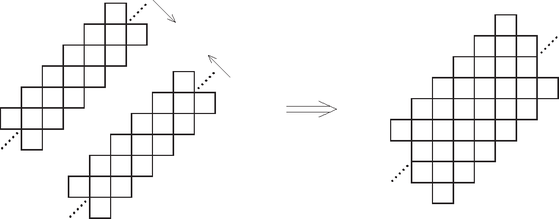
 
 

Végtelen sok ilyen lépcsős alakzat összetolásával az egész két kockányi vastagságú térrész kitöltése megoldható. Mivel sem alul, sem fölül nincsenek kilógó részek, azaz a kapott végtelen alakzat alap- és fedőlapja is sík, ilyen alakzatok egymásra helyezésével az egész tér kitölthető.
 
 
II. megoldás. Tekintsünk egy térbeli koordinátarendszert, ahol a testet alkotó kiskockák élei legyenek egységnyiek. Osszuk fel a teret tengelypárhuzamos, egység élű kockákra, melyek középpontjainak koordinátái egészek. A testtel úgy fogjuk kitölteni a teret, hogy annak kockái egybeessenek a fenti kiskockákkal. Ekkor a test nyilván valamelyik hat ilyen egységkockát fogja kitölteni teljes egészében és semmi mást. Mindegyik kiskocka egyértelműen megadható a középpontjainak koordinátáival, amik egészek, valamint minden (x;y;z) (x,y,z∈Z) számhármas egyértelműen megad egy ilyen egységkockát.
Minden x; y; z egész számra az (x;y;z); (x-1;y;z); (x+1;y;z); (x;y-1;z); (x;y+1;z); (x;y;z+1) koordináták által meghatározott egységkockák egyesítése egy megfelelő testet alkot. A továbbiakban csak azokat a testeket tekintsük, amelyekhez van ilyen (x;y;z) számhármas (x;y;z∈Z). Egy ilyen test már egyértelműen megadható a középső kiskockájának koordinátáival. Tekintsünk egy (x0;y0;z0) kiskockát (x0;y0;z0∈Z). Ez pontosan akkor lesz benne egy ilyen testben, ha annak (x;y;z) középső kockájára (x;y;z∈Z)
x=x0;y=y0;z=z0;x=x0-1;y=y0;z=z0;x=x0+1;y=y0;z=z0;x=x0;y=y0-1;z=z0;x=x0;y=y0+1;z=z0;vagyx=x0;y=y0;z=z0-1.  

Tekintsük most azon testeket, amik a korábbi feltételeknek megfelelnek és (x;y;z) koordinátájú középső kockájukra x+2y+3z≡0(mod  b). Az az állítás, hogy ezek a testek átfedések nélkül és hézagmentesen lefedik a teret. Ehhez nyilván elég belátni, hogy a térben minden egységkockát pontosan egyszer lefedtünk. Ez az előbbiek szerint pontosan akkor teljesül, ha minden (x0;y0;z0) kiskockára az (x0;y0;z0); (x0-1;y0;z0); (x0+1;y0;z0); (x0;y0-1;z0); (x0;y0+1;z0); (x0;y0;z0-1) kiskockák közül pontosan egy a középső kiskockája valamelyik testnek. A konstrukció miatt ennek az a pontos feltétele, hogy az x0+2y0+3z0; (x0-1)+2y0+3z0; (x0+1)+2y0+3z0; x0+2(y0-1)+3z0; x0+2(y0+1)+3z0; x0+2y0+3(z0-1) számok között mindig pontosan egy legyen osztható 6-tal. Ez pedig mindig teljesül, hiszen ez 6 egymást követő egész szám (ha az első szám k, akkor a számok rendre k, k-1, k+1, k-2, k+2, k-3).
Tehát ez a konstrukció valóban lefedi a teret átfedések nélkül és hézagmentesen.