Kezdőlap


Feladat:	B.4036	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Blázsik Zoltán , Gévay Gábor
Füzet:	2011/szeptember, 345 - 347. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Körülírt kör, Körérintők, Pitagorasz-tétel alkalmazásai, Thalesz tétel és megfordítása, Feladat
Hivatkozás(ok):	Feladatok: 2007/november: B.4036

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A két kör kívülről érinti egymást $P$ -ben, ezért az $O_{1}$ , $P$ és $O_{2}$ pontok egy egyenesre esnek.
A $k_{1}$ körnek az $e$ és az $f$ egyenes is érintője, és ezen érintők párhuzamosok. Ezért a két érintési pont, $A$ és $C$ által meghatározott húr egy átmérő, és így a Thalész-tétel szerint $A P C ∢ = 90^{\circ}$ .
Mivel a $C A B ∢ = 90^{\circ}$ , az $A B C$ háromszög köréírt körének a $B C$ egy átmérője. Legyen az $f$ egyenesnek az $A B C$ háromszög köréírt körével való másik metszéspontja $F$ . Belátjuk, hogy $F$ felezi a $D E$ szakaszt.
Mivel $B F C ∢ = 90^{\circ}$ , és a $B O_{2}$ egyenes is merőleges $f$ -re, azért $B$ , $O_{2}$ és $F$ egy egyenesre esik. Tehát $B F$ átmegy a $k_{2}$ kör középpontján, és merőleges $D E$ -re, ezért az $F$ pontban felezi azt. Ebből az is következik, hogy $B D = B E$ .
Vizsgáljuk az $A B F C$ téglalapot. Megmutatjuk, hogy $B A = B D$ . A $k_{1}$ kör sugara legyen $r$ , a $k_{2}$ kör sugara pedig $R$ . Jelölje $S$ az $O_{1}$ pontból a $B F$ egyenesre állított merőleges talppontját. Az 1. ábrán található $O_{1} O_{2} S$ , $O_{2} D F$ és $B D F$ derékszögű háromszögekre felírt Pitagorasz-tételek szerint:

\begin{matrix} {(R + r)}^{2} - {(R - r)}^{2} = A B^{2} \to A B^{2} = 4 r R, \\ D F^{2} = R^{2} - {(2 r - R)}^{2} = 4 r R - 4 r^{2}, \\ B D^{2} = D F^{2} + {(2 r)}^{2} = 4 r R = A B^{2} . \end{matrix}

Tehát beláttuk, hogy

B A = B D = B E

. Ebből következik, hogy az

A D E

háromszög köré írt kör középpontja a

B

pont.
Legyen

H

a két köréírt kör másik metszéspontja (az egyik

A

). Ekkor az is igaz, hogy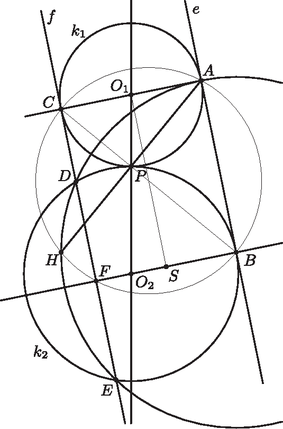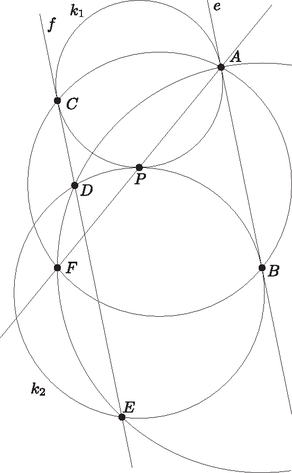

B A = B D = B E = B H

1. ábra

2. ábra

Mivel az

A B C

háromszög köréírt körének

B C

átmérője, azért a

B H C

háromszög is derékszögű, és mivel a

B C

oldaluk közös és

B A = B H

, az

A B C

és a

H B C

háromszögek egybevágóak. Vagyis az

A

illetve a

H

pontokból a

B C

-re bocsátott merőlegesek talppontja egy pontba (a

P

pontba) esik.
Ezzel beláttuk a feladat állítását, vagyis az

A H

közös húr tényleg tartalmazza a

P

pontot.

II. megoldás. Akalmazzunk egy

B

középpontú,

A B

sugarú inverziót. Az inverzió alapkörének és

k_{2}

-nek a metszéspontját jelölje

D_{1}

, illetve

E_{1}

.
Mivel

k_{2}

illeszkedik

B

-re, inverze a

D_{1} E_{1}

egyenes, azaz

k_{2}' = D_{1} E_{1}

. Mivel

B

a középpont, azért

D_{1} E_{1} ∥ A B

. Az

e

egyenes illeszkedik

B

-re, ezért invariáns. A

k_{1}

kör is invariáns, mert merőlegesen metszi az inverzió alapkörét. Ebből következik, hogy

k_{1}

érinti

k_{2}'

-t, ami pedig az

A B

-vel párhuzamos

D_{1} E_{1}

egyenes. Tehát

D_{1}

és

E_{1}

a feladatban szereplő

D

és

E

ponttal rendre megegyezik. Ezzel beláttuk, hogy az

A D E

háromszög köré írt kör középpontja

B

, vagyis az

A D E

háromszög köré írt kör az inverzió alapköre (2. ábra). A

k_{1}

kör és az

f

egyenes érintési pontja

C

. Az inverziónál

C'

k_{1}' = k_{1}

és az

f' = k_{2}

érintési pontja, vagyis

P

. Az

A B C

háromszög köré írt körének képe az

A P

egyenes. Ez az egyenes ezért közös húrja a körnek és az inverzió alapkörének, és éppen ezt kellett bizonyítani.