Feladat:	C.1052	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Iványi Roland ,  Madarasi Adrienn
Füzet:	2012/április, 215. oldal		PDF  |  MathML
Témakör(ök):	C gyakorlat, Síkgeometriai bizonyítások, Húrnégyszögek, Középponti és kerületi szögek, Thalesz tétel és megfordítása
Hivatkozás(ok):	Feladatok: 2010/november: C.1052

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.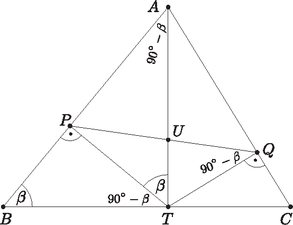   I. megoldás. Jelöljük az $ABT$ szöget $\beta$-val, ekkor $BAT\sphericalangle ={90}^{\circ }-\beta$, $BTP\sphericalangle ={90}^{\circ }-\beta$, $PTU\sphericalangle =\beta$.     Mivel $APT\sphericalangle =TQA\sphericalangle ={90}^{\circ }$, azért $APTQ$ húrnégyszög, azaz van köré írható köre. E kör $PT$ ívéhez két kerületi szög tartozik ($TAP\sphericalangle$; $TQP\sphericalangle$), ezért $TAP\sphericalangle =TQP\sphericalangle ={90}^{\circ }-\beta$. Vagyis $\begin{array}{c}{\displaystyle PQT\sphericalangle +TQC\sphericalangle +PBT\sphericalangle ={90}^{\circ }-\beta +{90}^{\circ }+\beta ={180}^{\circ }\mathrm{,}}\end{array}$   ezért a $BCQP$ húrnégyszög, mert szemben lévő szögeinek összege 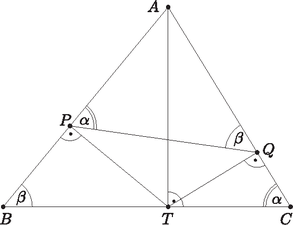${180}^{\circ }$.     II. megoldás. Az $ABT$ derékszögű háromszögre a befogó tételt alkalmazva: $A{T}^2=AP\cdot AB$, az $ATC$ háromszögre: $A{T}^2=AQ\cdot AC$. A két egyenletből következik:$AP\cdot AB=AQ\cdot AC$.     Az $APQ$ és az $ABC$ háromszögnek a $CAB$ közös szöge, másik két oldaluk aránya pedig megegyezik, így a két háromszög hasonló. Tudjuk, hogy $APQ\sphericalangle =ACB\sphericalangle =\alpha$, $AQP\sphericalangle =ABC\sphericalangle =\beta$, $QPB\sphericalangle ={180}^{\circ }-\alpha$, $PQC\sphericalangle ={180}^{\circ }-\beta$. A húrnégyszögek tétele alapján $PBCQ$ négyszög húrnégyszög, mert szemközti szögeinek összege ${180}^{\circ }$.