Kezdőlap


Feladat:	B.4224	Korcsoport: 16-17	Nehézségi fok: könnyű
Füzet:	2010/november, 475 - 476. oldal		PDF \| MathML
Témakör(ök):	Feladat, Rombuszok, Pitagorasz-tétel alkalmazásai, Másodfokú (és arra visszavezethető) egyenletrendszerek
Hivatkozás(ok):	Feladatok: 2009/december: B.4224

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Jelölje a rombusz átlóinak hosszát $e$ és $f$ . Az átlók merőlegesen felezik egymást, ezért az ábrán látható $A M B$ háromszög derékszögű, vagyis alkalmazhatjuk Pitagorasz tételét, mely szerint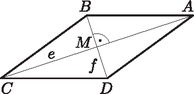

\begin{matrix} {(\frac{e}{2})}^{2} + {(\frac{f}{2})}^{2} = 2^{2}, azaz e^{2} + f^{2} = 16. \end{matrix}

Nyilván

0 < e f

, ezért

\begin{matrix} 16 = e^{2} + f^{2} < {(e + f)}^{2} \leq {(e + f)}^{2} + {(e - f)}^{2} = 2 (e^{2} + f^{2}) = 32, \end{matrix}

tehát

\begin{matrix} 4 < e + f \leq \sqrt[]{32} < 6. \end{matrix}

Ezért, ha

e + f

egész, akkor csak

e + f = 5

jöhet szóba.
Ilyen rombusz pontosan akkor létezik, ha az

e + f = 5

e^{2} + f^{2} = 16

egyenletrendszernek van megoldása a pozitív számok körében. Ha

e

és

f

megoldása az egyenletrendszernek, akkor

\begin{matrix} e f = \frac{{(e + f)}^{2} - (e^{2} + f^{2})}{2} = \frac{5^{2} - 16}{2} = 4, 5. \end{matrix}

Tehát a gyökök és együtthatók közti összefüggések alapján

e

és

f

\begin{matrix} x^{2} - 5 x + 4, 5 = 0 \end{matrix}

másodfokú egyenlet gyökei. Ennek megoldásai:

\begin{matrix} x_{1} = \frac{5 + \sqrt[]{7}}{2} \approx 3, 82, x_{2} = \frac{5 - \sqrt[]{7}}{2} \approx 1, 18. \end{matrix}

Ezek pozitív számok, ezért létezik a feltételeknek megfelelő rombusz, s az átlói hosszának összege 5.