Kezdőlap


Feladat:	C.1044	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Náhóczki Máté , Straubinger Dániel
Füzet:	2012/január, 12 - 13. oldal		PDF \| MathML
Témakör(ök):	C gyakorlat, Vektorok lineáris kombinációi, Síkgeometriai bizonyítások, Négyszögek középvonalai
Hivatkozás(ok):	Feladatok: 2010/szeptember: C.1044

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Vezessük be a következő vektorokat: $M$ -ből az $A$ , $B$ , $C$ , illetve $D$ -be mutató vektorok legyenek $a$ , $b$ , $c$ , illetve $d$ . Jelölje az 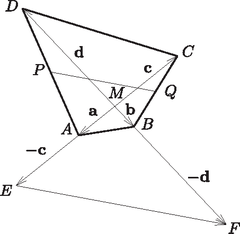$A D$ oldal felezőpontját $P$ , a $B C$ oldal felezőpontját $Q$ . Ekkor

\begin{matrix} \vec{M P} = \frac{a + d}{2} és \vec{M Q} = \frac{b + c}{2} . \end{matrix}

Így

\begin{matrix} \vec{Q P} = \vec{M P} - \vec{M Q} = \frac{a + d - b - c}{2} . & (1) \end{matrix}

\vec{F E}

felírható az

\vec{M E}

és

\vec{M F}

vektorok különbségeként, azaz

\begin{matrix} \vec{F E} = \vec{M E} - \vec{M F} = a - c - (b - d) = a + d - b - c . \end{matrix}

(

| \vec{M C} | = | \vec{A E} |

, az

E

A

C

pontok egy egyenesen vannak, és

\vec{A E} = - c

hosszuk egyenlő, irányuk ellentétes. Hasonló igaz a

\vec{B F}

-re is.)
A kapott egyenlőséget (1)-gyel összevetve kapjuk, hogy

\vec{E F} = 2 \vec{P Q}

, és így

P Q ∥ E F

, és ezt akartuk bizonyítani.

II. megoldás. Az

A B

oldal felezőpontját jelöljük

X

-szel. Az

A D

oldal felezőpontja legyen

Y

, és a

B C

oldalé

Z

.
Az

A B D

háromszögben

X Y ∥ B D

és

X Y = \frac{1}{2} B D

. Hasonlóan az

A B C

háromszögben

X Z ∥ A C

és

X Z = \frac{1}{2} A C

. Az

E M F ∢

-et jelöljük

γ

-val, legyen

Y X Z ∢ = γ'

. Mivel

X Y ∥ B D

és

X Z ∥ A C

, így

γ

és

γ'

párhuzamos szárú szögek, egy parallelogramma szemköztes szögei, s ezért egyenlők.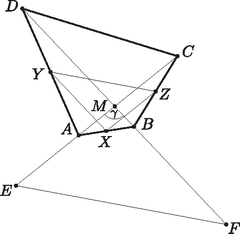

Ebből következik, hogy az

E M F

háromszög hasonló a

Z X Y

háromszöghöz, két megfelelő oldaluk párhuzamos, és hosszuk aránya

2 : 1

. Ezért a harmadik oldaluk is párhuzamos, és ezt akartuk bizonyítani.