Feladat:	4681. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Berta Dénes ,  Kaposvári Péter
Füzet:	2015/február, 111 - 117. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Egyéb ellenállás-kapcsolások
Hivatkozás(ok):	Feladatok: 2014/november: 4681. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. A feladatban szereplő szalag $A$ és $B$ pontja közötti (egységnyi nagyságúnak tekinthető) ellenállást helyettesíthetjük a szalag mindkét végét lezáró, egyenként 2 egységnyi ellenállással. Ezek párhuzamos eredője ugyanis (a szalag végeinek összekapcsolása után) az eredeti, egyetlen 1 egységnyi ellenállással egyenlő. Ha az így átalakított lánc egyik végére valamekkora $U$ feszültséget kapcsolunk, a másik végének két pontja közé pedig ‐ valamilyen polaritással ‐ ugyanakkora ($\pm U$) feszültséget kötünk, akkor lánc két végének összekapcsolásától akár el is tekinthetünk; a kialakuló árameloszlás (és az abból kiszámolható eredő ellenállás) az összekapcsolt és az összekapcsolatlan ellenállásláncra ugyanaz lesz. Az azonos polaritású feszültségforrásokra kapcsolt (sima) szalagban a felező egyenesre nézve tengelyesen szimmetrikus, az ellentétes polaritású feszültségre kapcsolt (Möbius-) szalagban pedig annak $O$ középpontjára nézve centráliusan (középpontosan) szimmetrikus feszültségeloszlás alakul ki. Az azonos potenciálú pontokat összekapcsolhatjuk, és ha így két pont közé két darab 1 egységnyi ellenállás kerül párhuzamosan kapcsolva, ezeket helyettesíthetjük egyetlen $\frac{1}{2}$ egységnyi ellenállással. Az alábbi ábrákon az 1 egységnyi ellenállást üres téglalappal, az $\frac{1}{2}$ egységnyi ellenállást pedig szürke téglalappal fogjuk jelölni. Ha $N$ páros, akkor az 1. ábrán látható két helyzet jön létre (az azonos betűkkel jelölt pontok azonos potenciálúak). Ezeket a kapcsolásokat a 2. ábrán bemutatott módon alakíthathatjuk át. Jól látszik, hogy az $A$ és $B$ közötti eredő ellenállás az $a)$ esetben nagyobb, mint a $b)$ esetnek megfelelő Möbius-szalagnál, hiszen a két kapcsolás csak a jobb oldali utolsó ágban különbözik egymástól, és az a $b)$ esetben kisebb ellenállású. (Kihasználtuk, hogy a $b)$ esetben a centrális szimmetria miatt az $S$ és $T$ pont azonos potenciálú, a közöttük lévő ellenállás tehát rövidzárral is helyettesíthető.) 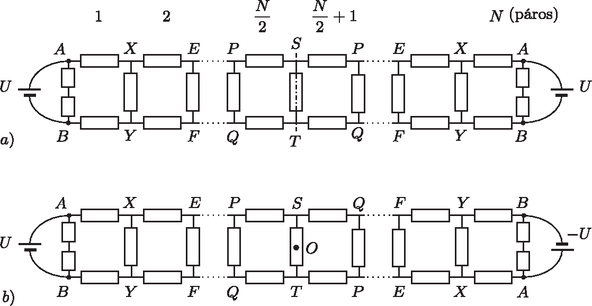  1. ábra 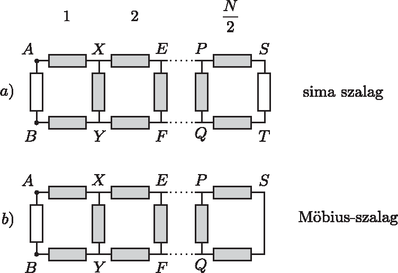    2. ábra   A páratlan $N$-nek megfelelő kapcsolásokat a 3. ábra mutatja. 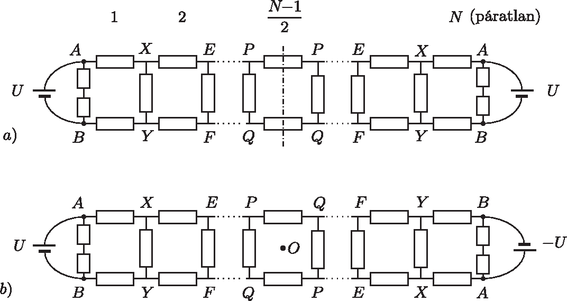  3. ábra   Az ekvipotenciális pontok összekötése után kialakuló kapcsolások a (4. ábrán) láthatók. Most is a $b)$ esetben lesz kisebb az $A$ és $B$ pontok közötti eredő ellenállás, hiszen csak a jobb szélső ágban különbözik a két kapcsolás, és a szélső ág ellenállása a Möbius-szalagos kapcsolásban a kisebb. 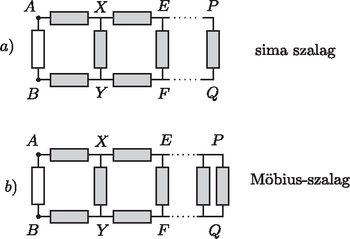  4. ábra     II. megoldás. Az $A$ és $B$ pontok közötti ellenállást eltávolíthatjuk a kapcsolásból, és vizsgálhatjuk az így kapott ,,csonkított'' (a jobb és a bal oldal felcserélésére nézve szimmetrikus) elrendezést. (A kisebb-nagyobb reláció szempontjából ez a csonkítás nyilván lényegtelen, hiszen ha a maradék lánc eredő ellenállása valamelyik esetben nagyobb, az eltávolított ellenállással együtt is ugyanebben az esetben lesz nagyobb csonkított rész és az eltávolított ellenállás párhuzamos eredője.) Kapcsoljunk az $A$ és $B$ pontok közé valamekkora (mondjuk $U$ nagyságú) feszültséget, és vizsgáljuk meg, mekkora teljesítményt vesz fel az egész ellenálláslánc. Ezt a teljesítményt kétféle módon is kiszámíthatjuk: $\begin{array}{c}{\displaystyle P=\frac{U^2}{R_{\text{eredő}}}=R_0\sum _k^{}{I}_k^2\mathrm{,}}\end{array}$ ahol $R_0$ az egyforma ellenállások nagysága, $I_k$ pedig a $k$-adik ellenálláson átfolyó áram erőssége. (A $k$-ra vett összegzés a teljes láncra, annak minden elemére vonatkozik.) Látható, hogy annál a kapcsolásnál lesz kisebb az eredő ellenállás, amelyiknél az áramerősségek négyzetösszege nagyobb. Belátjuk, hogy ez a Möbius-szalagra teljesül, vagyis $\begin{array}{c}{\displaystyle \sum _{\text{Möbius}}^{}{I}^2>\sum _{\text{sima}}^{}{I}^2\mathrm{,}}\end{array}$ (1) és emiatt $\begin{array}{c}{\displaystyle R_{\text{eredő}}^{\text{(Möbius-szalag)}}<R_{\text{eredő}}^{\text{(sima szalag)}}\mathrm{.}}\end{array}$ (2) Tekintsük először az 5. ábrán látható elrendezést, amelyben a szalag bal oldalára adott nagyságú feszültséget kapcsolunk, a jobb oldali kivezetéseit pedig rövidre zárjuk. A kialakuló áramerősségeket az ábrán látható módon jelöljük. 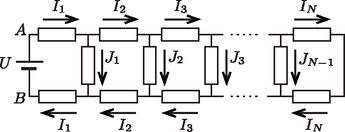  5. ábra   Ha ugyanezt a kapcsolást a jobb és a bal oldal felcserélésével állítjuk össze, abban a 6. ábrán látható áramok fognak folyni. 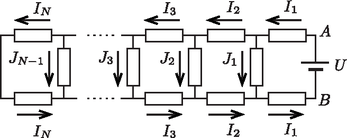  6. ábra   Szuperponáljuk egymásra (a megfelelő feszültségek és áramerősségek összeadásával) az 5. és a 6. ábrán látható elrendezést! Ekkor a két-két végpont azonos potenciálú lesz, tehát az eredeti feladat $a)$ kérdésében szereplő módon össze is köthetjük azokat. A kialakuló áramerősségeket a 7. ábra mutatja. Eszerint a sima szalag ellenállásaiban folyó áramerősségek négyzetösszege: 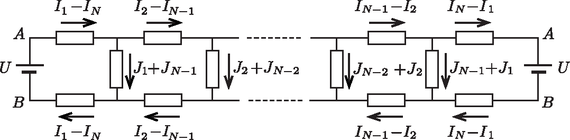$\begin{array}{c}{\displaystyle \sum _{\text{sima}}^{}{I}^2=2\sum _{i=1}^N{\left(I_i-I_{N+1-i}\right)}^2+\sum _{i=1}^{N-1}{\left(J_i+J_{N-i}\right)}^2\mathrm{.}}\end{array}$ (3)   7. ábra   Hasonló módon kapjuk meg a Möbius-szalag megfelelő kifejezéseit is. Ha a 6. ábrán látható kapcsolásban $-U$ feszültséget kötünk a szalag jobb szélére, valamennyi áramerősség iránya megváltozik. A ,,szuperponált'' elrendezésben a bal és a jobb oldali végpontok potenciálja ,,keresztirányban'' egyezik meg egymással, tehát a $b)$ esetnek megfelelően Möbius-szalagként kapcsolható össze az ellenálláslánc (8. ábra). Ennek megfelelően az áramok négyzetösszege: 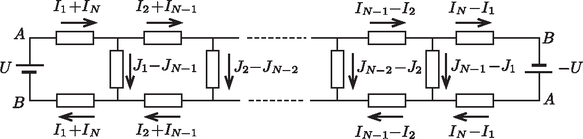$\begin{array}{c}{\displaystyle \sum _{\text{Möbius}}^{}{I}^2=2\sum _{i=1}^N{\left(I_i+I_{N+1-i}\right)}^2+\sum _{i=1}^{N-1}{\left(J_i-J_{N-i}\right)}^2\mathrm{.}}\end{array}$ (4)   8. ábra   Behelyettesítve (3)-at és (4)-et a bizonyítandó (1) egyenlőtlenségbe a négyzetes tagok kiejtése és egyszerűsítések után kapjuk, hogy $\begin{array}{c}{\displaystyle 2I_1\cdot I_N+\sum _{i=1}^{N-1}\left(2I_i\cdot I_{N+1-i}-J_i\cdot J_{N-i}\right)>0.}\end{array}$ Ez az egyenlőtlenség biztosan igaz, ha a zárójelben szereplő tagok mindegyike pozitív, vagyis ha: $\begin{array}{c}{\displaystyle {\alpha }_i\equiv \frac{2I_i}{J_i}>\frac{J_{N-i}}{I_{N+1-i}}\equiv {\beta }_{N-i}\mathrm{.}}\end{array}$ (5) Belátjuk, hogy a fenti egyenlőtlenség valóban teljesül, mert az ${\alpha }_i$ arányszámok mindegyike nagyobb, mint $1+\sqrt[]{3}$, a ${\beta }_i$ számok pedig mind kisebbek, mint $1+\sqrt[]{3}$ ($i=\mathrm{1,2,3,}\text{...}$). Kapcsoljunk az 5. ábrán látható láncra akkora feszültséget, hogy a legutolsó (a jobb szélső) ágban 1 egységnyi legyen az áramerősség (9. ábra). 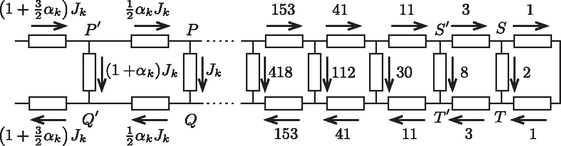  9. ábra   Mivel a láncszemek $R_0$ ellenállását is egységnyinek választhatjuk, az utolsó 2 ellenálláson 2 egységnyi feszültség esik, emiatt az $S$ és $T$ pontok közötti ,,létrafokon'' átfolyó áram is 2 egységnyi. A csomóponti törvény szerint az $S$ pontba befolyó és a $T$ pontból kifolyó áram erőssége 3 egység, az $S\text{'}$ és $T\text{'}$ pontok közti feszültségesés tehát $3+2+3=8$ egység, és ugyanekkora áram folyik $S\text{'}$ és $T\text{'}$ között, és így tovább fokonként meghatározhatók az áramerősségek. Kiszámíthatjuk, hogy ${\displaystyle \begin{array}{cccc}\hfill {\displaystyle {\alpha }_{N-1}}& {\displaystyle =2\cdot \frac{3}{2}=3\mathrm{,}\mathrm{000,}}\hfill & {\displaystyle {\beta }_1}\hfill & \hfill {\displaystyle =\frac{2}{1}=2\mathrm{,}000;}\\ \hfill {\displaystyle {\alpha }_{N-2}}& {\displaystyle =2\cdot \frac{11}{8}=2\mathrm{,}\mathrm{750,}}\hfill & {\displaystyle {\beta }_2}\hfill & \hfill {\displaystyle =\frac{8}{3}=2\mathrm{,}667;}\\ \hfill {\displaystyle {\alpha }_{N-3}}& {\displaystyle =2\cdot \frac{41}{30}=2\mathrm{,}\mathrm{733,}}\hfill & {\displaystyle {\beta }_3}\hfill & \hfill {\displaystyle =\frac{30}{11}=2\mathrm{,}727;}\\ \hfill {\displaystyle {\alpha }_{N-4}}& {\displaystyle =2\cdot \frac{153}{112}=2\mathrm{,}\mathrm{7321,}}\hfill & {\displaystyle {\beta }_4}\hfill & \hfill {\displaystyle =\frac{112}{41}=2\mathrm{,}\mathrm{7317,}}\end{array}}$ vagyis az egyik sorozat monoton csökken, a másik monoton növekszik, és (sejthetően) egyre jobban megközelítik az idézett $1+\sqrt[]{3}\approx 1\mathrm{,}7320$ ,,határértéket''. Ha a lánc valamelyik ágában (pl. a 9. ábrán látható $P$ és $Q$ pontok között) $J_k$ áram folyik, és ismerjük az ehhez az ághoz tartozó ${\alpha }_k$ arányszámot, akkor a Kirchhoff-féle hurok- és csomóponti törvényből kiszámíthatjuk a szomszédos $P\text{'}$ és $Q\text{'}$ pontok közötti áram erősségét is, és innen a szomszédos ághoz tartozó $\alpha$-arányt: $\begin{array}{c}{\displaystyle {\alpha }_{k-1}=\frac{2+3{\alpha }_k}{1+{\alpha }_k}\mathrm{.}}\end{array}$ Ennek a rekurziós formulának ${\alpha }^{*}$ ,,fixpontja'' az ${\alpha }_{k-1}={\alpha }_k$ egyenlet (pozitív) gyökeként adódik: $\begin{array}{c}{\displaystyle {\alpha }^{*}=\frac{2+3{\alpha }^{*}}{1+{\alpha }^{*}}\mathrm{,}\text{ahonnan}{\alpha }^{*}=1+\sqrt[]{3.}}\end{array}$ Algebrai átalakítások után könnyen megkapható, hogy ${\alpha }_{k-1}<{\alpha }_k$ (tehát $k$ csökkenésével a sorozat elemei monoton csökkennek), és ${\alpha }_{k-1}>{\alpha }^{*}$, ha ${\alpha }_k>{\alpha }^{*}$. Hasonló lépésekkel láthatjuk be, hogy a monoton növekvő (${\beta }_{k+1}>{\beta }_k$) sorozatnak is ${\alpha }^{*}$ a ,,fixpontja'', és teljesül ${\beta }_{k+1}<{\alpha }^{*}$, ha ${\beta }_k<{\alpha }^{*}$. Ezek szerint az (5) egyenlőtlenség valóban fennáll, vagyis (1) bizonyítást nyert. Ezzel beláttuk, hogy a megcsavarás nélkül összekapcsolt szalag (,,létra'') bármelyik fokának végpontjai között nagyobb az eredő ellenállás, mint a megcsavart Möbius-szalag valamelyik fokának végpontjai közötti eredő ellenállás.