Feladat:	4655. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Gnädig Péter ,  Molnár Szilárd
Füzet:	2015/február, 107 - 108. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Pontrendszerek mozgásegyenletei
Hivatkozás(ok):	Feladatok: 2014/szeptember: 4655. fizika feladat

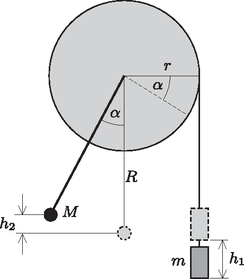
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.       Megoldás. $a)$ Az ábrán látható, $\alpha ={60}^{\circ }$-os szögelfordulásnak megfelelő helyzetben az $m$ tömegű test az eredeti helyzetéhez képest $\begin{array}{c}{\displaystyle h_1=r\alpha =0\mathrm{,}1\text{m}\cdot \frac{\pi }{3}=0\mathrm{,}105\text{m}}\end{array}$ szinttel mélyebbre, a $M$ tömegű test pedig $\begin{array}{c}{\displaystyle h_2=R\left(1-\text{cos}\alpha \right)=0\mathrm{,}1\text{m}}\end{array}$ szintkülönbségnek megfelelő értékkel magasabbra kerül. Mivel a mozgási energia kezdetben is és ebben az állapotban is nulla, a rendszer helyzeti energiája sem változhatott meg: $\begin{array}{c}{\displaystyle \Delta E_{\text{h}}=Mg{h}_2-mg{h}_1=\mathrm{0,}}\end{array}$ ahonnan a rúdon lévő test tömege: $\begin{array}{c}{\displaystyle M=\frac{h_1}{h_2}m=105\text{g. }}\end{array}$ $b)$ Az új egyensúlyi helyzetet a forgatónyomatékok egyensúlya jellemzi: $\begin{array}{c}{\displaystyle mgr=MgR\text{sin}\phi \mathrm{,}}\end{array}$ vagyis $\begin{array}{c}{\displaystyle \text{sin}\phi =\frac{mr}{MR}\approx 0\mathrm{,}48;\phi \approx 28\mathrm{,}{6}^{\circ }\mathrm{.}}\end{array}$ $c)$ Az egyensúlyi állapottól $\Delta \phi$ szöggel eltérő helyzetben (vagyis amikor a rúd $\phi +\Delta \phi$ szöget zár be a függőlegessel) a rendszerre ható forgatónyomaték: $\begin{array}{c}{\displaystyle M\left(\Delta \phi \right)=mgr-MgR\text{sin}\left(\phi +\Delta \phi \right)=mgr-MgR\left(\text{sin}\phi \text{cos}\Delta \phi +\text{cos}\phi \text{sin}\Delta \phi \right)\mathrm{.}}\end{array}$ Kihasználva, hogy kicsiny szögeknél $\text{cos}\Delta \phi \approx 1$ és $\text{sin}\Delta \phi \approx \Delta \phi$, a forgatónyomaték így írható: $\begin{array}{c}{\displaystyle M\left(\Delta \phi \right)=\left[mgr-MgR\text{sin}\phi \right]-MgR\text{cos}\phi \cdot \Delta \phi \mathrm{.}}\end{array}$ A szögletes zárójelben álló kifejezés az egyensúlyi feltétel miatt nulla, a forgatónyomaték tehát $\begin{array}{c}{\displaystyle M\left(\Delta \phi \right)=-D^{*}\Delta \phi \mathrm{,}}\end{array}$ ahol $D^{*}=MgR\text{cos}\phi$ az ún. direkciós forgatónyomaték. A forgómozgás alapegyenlete szerint: $\begin{array}{c}{\displaystyle M=\Theta \beta \mathrm{,}}\end{array}$ ahol $\Theta =M{R}^2+m{r}^2$ a rendszer tehetetlenségi nyomatéka, $\beta$ pedig a pillanatnyi szöggyorsulás. A szögelfordulás időbeli változását leíró $\Theta \beta =-D^{*}\Delta \phi$ egyenlet és a rezgőmozgás $ma=-D\Delta x$ egyenletének hasonló alakjából leolvashatjuk, hogy a csavarodási rezgések periódusideje: $\begin{array}{c}{\displaystyle T=2\pi \sqrt[]{\frac{\Theta }{D^{*}}}=2\pi \sqrt[]{\frac{M{R}^2+m{r}^2}{MgR\text{cos}\phi }}\approx 1\mathrm{,}1\text{s. }}\end{array}$   Megjegyzés. A $c)$ alkérdésre energetikai megfontolások alapján is válaszolhatunk. Ha a rendszert $\Delta \phi$ szöggel kitérítjük az egyensúlyi helyzetéből, a helyzeti energia változása (a kis szögekre vonatkozó közelítő képletek alkalmazásával): ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \Delta E_{\text{h}}}& {\displaystyle =E_{\text{h}}\left(\phi +\Delta \phi \right)-E_{\text{h}}\left(\Delta \phi \right)=MgR\text{cos}\phi -MgR\text{cos}\left(\phi +\Delta \phi \right)-mgr\Delta \phi =}\hfill \\ \hfill {\displaystyle }& {\displaystyle =MgR\text{cos}\phi \left(1-\text{cos}\Delta \phi \right)+MgR\text{sin}\phi \text{sin}\Delta \phi -mgr\Delta \phi \approx }\hfill \\ \hfill {\displaystyle }& {\displaystyle \approx MgR\text{cos}\phi \cdot 2\text{sin}{}^2\frac{\Delta \phi }{2}+\left[MgR\text{sin}\phi -mgr\right]\Delta \phi \approx \frac{1}{2}MgR\text{cos}\phi \cdot {\left(\Delta \phi \right)}^2\mathrm{.}}\hfill \end{array}}$ (Kihasználtuk, hogy a szögletes zárójelben álló kifejezés az egyensúlyi feltétel szerint 0.) Látható, hogy az egyensúlyi helyzetéből kitérített rendszer helyzeti energiája a kitérés négyzetével arányos, éppen úgy, mint egy megnyújtott rugó rugalmas energiája. Emiatt állíthatjuk, hogy mindkét test harmonikus rezgőmozgást fog végezni, a $m$ tömegű test rezgési amplitúdója $A_1=r\Delta \phi$, a $M$ tömegű testé pedig $A_2=R\Delta \phi$ lesz, amennyiben $\Delta \phi$ a maximális szögkitérés. Ha a rezgőmozgás körfrekvenciája $\omega =\left(2\pi \right)/T$, akkor az egyensúlyi helyzeten való áthaladáskor a mozgási energia: $\begin{array}{c}{\displaystyle E_{\text{m}}=\frac{1}{2}m{\left(A_1\omega \right)}^2+\frac{1}{2}M{\left(A_2\omega \right)}^2=\frac{1}{2}\left(m{r}^2+M{R}^2\right){\omega }^2{\left(\Delta \phi \right)}^2\mathrm{.}}\end{array}$ A helyzeti és a mozgási energia legnagyobb értékeinek egyenlőségéből a körfrekvenciára $\begin{array}{c}{\displaystyle {\omega }^2=\frac{MgR\text{cos}\phi }{m{r}^2+M{R}^2}\mathrm{,}}\end{array}$ a periódusidőre pedig $\begin{array}{c}{\displaystyle T=\frac{2\pi }{\omega }=2\pi \sqrt[]{\frac{m{r}^2+M{R}^2}{MgR\text{cos}\phi }}\approx 1\mathrm{,}1\text{s }}\end{array}$ adódik.