Feladat:	4648. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Antalicz Balázs ,  Gnädig Péter
Füzet:	2015/január, 52 - 54. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Elektromos fluxus (erővonalszám)
Hivatkozás(ok):	Feladatok: 2014/május: 4648. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.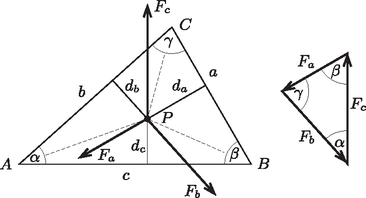   I. megoldás. Tekintsük a pálcák által kijelölt háromszög egy belső $\left(P\right)$ pontját, és rajzoljuk be az oda helyezett ponttöltésre ható erőket!     Azt a pontot keressük, ahol a ponttöltésre ható elektrosztatikus erők kiegyenlítik egymást, azaz vektori összegük zérus. (Ilyen pont nyilván csak a pálcák által alkotott síkban és a háromszög belsejében lehet.) Erőegyensúly esetén az egymás végébe rajzolt erővektorok záródó háromszöget alkotnak (lásd az ábra jobb oldali részét). Mivel mindegyik erővektor merőleges a háromszög valamely oldalára, az erővektorok alkotta háromszög és az eredeti háromszög hasonló. Így a megfelelő oldalaik aránya megegyezik: $\begin{array}{c}{\displaystyle \frac{F_a}{a}=\frac{F_b}{b}=\frac{F_c}{c}\mathrm{.}}\end{array}$ (1) Számítsuk most ki, hogy mekkora elektromos térerősség alakul ki egyetlen, nagyon hosszú, egyenletesen feltöltött (hosszegységenként $\eta$ töltéssel rendelkező) szigetelő pálca környezetében, a pálcától $r$ távolságban. A térerősség ‐ a szimmetria miatt ‐ a pálcára merőleges és mindenhol ugyanakkora $E\left(r\right)$ nagyságú. Alkalmazzuk az elektromos fluxus és a töltés nagysága között fennálló Gauss-törvényt egy $L$ hosszúságú, a pálcával azonos szimmetriatengelyű, $r$ sugarú hengerre: $\begin{array}{c}{\displaystyle E\left(r\right)\cdot 2\pi rL=\frac{1}{{\epsilon }_0}\eta L\mathrm{,}}\end{array}$ ahonnan $\begin{array}{c}{\displaystyle E\left(r\right)=\frac{\eta }{2\pi {\epsilon }_0}\cdot \frac{1}{r}\sim \frac{1}{r}\mathrm{.}}\end{array}$ Ezek szerint az egyes (ugyanakkora töltéssűrűségű) pálcák által a ponttöltésre kifejtett erő és a pálcától mért távolság szorzata ugyanakkora. Az ábra jelöléseit követve: $\begin{array}{c}{\displaystyle d_a{F}_a=d_b{F}_b=d_c{F}_c\mathrm{,}}\end{array}$ amit az (1) arányosságokkal összevetve $\begin{array}{c}{\displaystyle a\cdot d_a=b\cdot d_b=c\cdot d_c}\end{array}$ adódik, vagyis a háromszög csúcsaiból a $P$ pontba húzott szakaszok a háromszöget egyenlő területű részekre osztják. Ilyen tulajdonságú pont a háromszög belsejében csak egy van: a háromszög súlypontja. Nézzük ennek bizonyítását! Az $APB$ háromszög területe egyharmada az $ABC$ háromszög területének, emiatt $d_c$ megegyezik a $c$ oldalhoz tartozó magasság egyharmadával. Ezek szerint a $P$ rajta lesz az $a$ oldalhoz tartozó magasságnak az $a$ oldalhoz közelebbi harmadoló merőlegesén, és erre a harmadoló merőlegesre a háromszög $S$ súlypontja is illeszkedik. Mivel az oldalak helyzete szimmetrikus, ugyanez igaz egy másik, például a $b$ oldalhoz tartozó magasságra is. A két harmadoló egyenesnek egyetlen metszéspontja van, a feladat egyetlen megoldása tehát a háromszög súlypontja.   II. megoldás. Az elektrosztatikus erők egyensúlyának megkeresése egyenértékű feladat az elektrosztatikus potenciál szélsőértékének meghatározásával. Egy végtelen hosszú egyenesnek tekintehető, egyenletesen töltött szigetelő pálca potenciálja a pálcától mért távolság logaritmusával arányos: $\begin{array}{c}{\displaystyle U\left(r\right)=-\int (E\left(r\right)\text{d}r=\text{állandó}\cdot \text{ln}r+\text{állandó}\mathrm{.}}\end{array}$ A három (ugyanakkora töltéssűrűségű) pálca elektromos potenciálja az egyes pálcák potenciáljának összege: $\begin{array}{c}{\displaystyle U_{\text{eredő}}=U_1+U_2+U_3=\text{állandó}\cdot \text{ln}\left(d_a{d}_b{d}_c\right)+\text{állandó}\mathrm{.}}\end{array}$ Ez a kifejezés akkor legnagyobb (vagy legkisebb), ha a kérdéses pontban az oldalaktól mért távolságok szorzata maximális. Ezen szélsőérték-feladat megoldása: a háromszög súlypontja (lásd a B. 4636. feladat megoldását a 25. oldalon! ‐ a Szerk.).   Megjegyzés. A potenciálfüggvény menetéből az egyensúlyi helyzet stabilitására is következtethetünk. Ha a pálcák töltése és a ponttöltés előjele megegyezik, akkor a pálcák síkjában történő elmozdulásokra nézve az egyensúly stabil, a síkra merőlegesen viszont instabil. Ellentétes előjel esetén a helyzet fordított: a pálcák síkjából kitérített ponttöltést az elektromos erőtér visszahúzza, a pálcák síkjában történő elmozdulás hatására viszont valamelyik pálca magához rántja a ponttöltést. Ezek szerint semmilyen előjelű pálca eredő elektrosztatikus erőterében sem alakulhat ki minden irányban stabil egyensúlyi helyzet. Ez az állítás a nevezetes Earneshaw-tétel speciális esete.