Kezdőlap


Feladat:	2014. évi Nemzetközi Fizika Diákolimpia 1. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	2014/november, 489 - 494. oldal		PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia, Egyéb kényszermozgás, Egyéb fajhő, Görbületi nyomás, Váltóáram
Hivatkozás(ok):	Feladatok: 2014/október: 2014. évi Nemzetközi Fizika Diákolimpia 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A rész. Az 1. ábra mutatja a kis testre és a csőre ható erőket: az $m$ tömegű kis testre az $m g$ nehézségi erő és az $N$ nyomóerő, az $M$ tömegű csőre az $M g$ nehézségi erő, a talaj $F$ nyomóereje, az $S$ tapadási súrlódási erő és a kis test által kifejtett $- N$ nyomóerő hat.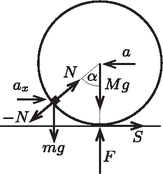

1. ábra. A kis testre és a csőre ható erők

Írjuk fel a mozgásegyenletet a kis test

a_{x}

vízszintes (az ábrán jobbra mutató) gyorsuláskomponensére, a cső tömegközéppontjának

a

(az ábrán balra mutató) gyorsulására és a cső

β

szöggyorsulására:

\begin{matrix} m a_{x} & = N sin α, \\ M a & = N sin α - S, \\ Θ β & = S R, \end{matrix}

ahol

Θ = M R^{2}

a cső tehetetlenségi nyomatéka. A cső gyorsulása és szöggyorsulása között a tiszta gördülés miatt fennáll az

a = β R

kapcsolat.
Az egyenletrendszert megoldva a testek gyorsulásai között az

m a_{x} = 2 M a

összefüggés adódik. A testek kezdetben nyugalomban voltak, és ez az összefüggés a mozgás során mindvégig fennáll, így a kis test

u

vízszintes sebességkomponense és a cső

v

sebessége között is ugyanilyen kapcsolat áll fenn:

m u = 2 M v

.
A rendszer konzervatív, így teljesül az energiamegmaradás tétele. Az egyenletet a kezdeti állapotra és arra a pillanatra írjuk fel, amikor a kis test éppen legalul van (és csak vízszintes irányban mozog):

\begin{matrix} m g R = \frac{m u^{2}}{2} + \frac{M v^{2}}{2} + \frac{Θ ω^{2}}{2}, \end{matrix}

ahol

ω

a cső szögsebessége, és a tiszta gördülés miatt

v = ω R

.
Az egyenletekből kifejezhetjük a kis test és a cső sebességét abban a pillanatban, amikor a kis test épp legalul van:

\begin{matrix} u = 2 \sqrt[]{\frac{M g R}{2 M + m}}, v = \frac{m}{M} \sqrt[]{\frac{M g R}{2 M + m}} . \end{matrix}

Vizsgáljuk a kis test mozgását a cső tömegközéppontjával együttmozgó vonatkoztatási rendszerben: itt a kis test

R

sugarú pályán körmozgást végez. A pálya legalján a sebessége

v_{rel} = u + v

, centripetális gyorsulása pedig

\begin{matrix} a_{cp} = \frac{v_{rel}^{2}}{R} = \frac{{(u + v)}^{2}}{R} . \end{matrix}

Ebben a pillanatban a cső gyorsulása nulla, így a kis test gyorsulása a talajhoz rögzített vonatkoztatási rendszerben is ugyanekkora. Így a kis testre vonatkozó mozgásegyenlet:

m a_{cp} = F - m g

, amiből a keresett

F

erő:

\begin{matrix} F = 3 m g (1 + \frac{m}{3 M}) . \end{matrix}

B rész. 1) A termodinamika első főtétele alapján a gáz által felvett

δ Q

hő

\begin{matrix} δ Q = n C_{V} d T + p d V, \end{matrix}

a keresett

C

moláris hőkapacitás pedig

\begin{matrix} C = \frac{1}{n} \frac{δ Q}{d T} = C_{V} + \frac{p}{n} \frac{d V}{d T} . \end{matrix}

Az egyenletekben

C_{V}

az állandó nyomáson mért moláris hőkapacitás,

p

n

V

és

T

pedig a buborékban lévő gáz nyomása, mólszáma, térfogata és hőmérséklete.
A Laplace-képlet alapján

\begin{matrix} p = \frac{4 σ}{r}, \end{matrix}

és eszerint a buborékban lévő gáz állapotváltozása egy olyan politropikus folyamat, melyre

p^{3} V = állandó

. Ezt összevetve az ideális gáz

p V = n R T

állapotegyenletével kapjuk, hogy

\begin{matrix} T^{3} V^{- 2} = állandó, \end{matrix}

amit differenciálva

\begin{matrix} \frac{d V}{d T} = \frac{3 V}{2 T} . \end{matrix}

Behelyettesítve ezt az eredményt a moláris hőkapacitás képletébe:

\begin{matrix} C = C_{V} + \frac{p}{n} \frac{3 V}{2 T} = C_{V} + \frac{3}{2} R, \end{matrix}

majd felhasználva, hogy a kétatomos gáz állandó térfogaton mért moláris hőkapacitása

\begin{matrix} C_{V} = \frac{5}{2} R, \end{matrix}

a keresett moláris hőkapacitás

\begin{matrix} C = \frac{5}{2} R + \frac{3}{2} R = 4 R = 33, 2 \frac{J}{mol K} . \end{matrix}

2) Mivel a gáz hőkapacitása sokkal kisebb, mint a buborék hőkapacitása, valamint a gáz és a buborék között jó hőkontaktus van, a gáz állapotváltozása izotermikusnak tekinthető.
Egyensúlyi állapotban a gáz

p

nyomása megegyezik az

r

sugarú buborék

p_{g}

görbületi nyomásával:

\begin{matrix} p = p_{g} = \frac{4 σ}{r} . \end{matrix}

Tekintsük a szappanhártya kicsiny

A

felületű darabját. Ennek tömege

\begin{matrix} m = ρ A h . \end{matrix}

Ha a buborék sugarának kicsiny megváltozását

x

-szel jelöljük, akkor a felületdarabkára felírt mozgásegyenlet:

\begin{matrix} m \ddot{x} \approx (p' - p_{g}') A, \end{matrix}

ahol

p'

a gáz nyomása,

p_{g}'

a görbületi nyomás az

r + x

sugarú buborékban.
Az izotermikus állapotváltozás miatt

p' V' = p V

, amiből

\begin{matrix} p' = p \frac{1}{{(1 + \frac{x}{r})}^{3}} \approx p (1 - \frac{3 x}{r}) = p_{g} (1 - \frac{3 x}{r}) . \end{matrix}

A görbületi nyomás

\begin{matrix} p_{g}' = \frac{4 σ}{r + x} \approx p_{g} (1 - \frac{x}{r}) . \end{matrix}

Behelyettesítve a mozgásegyenletbe:

\begin{matrix} ρ A h \ddot{x} = p_{g} (- \frac{2 x}{r}) A, \ddot{x} = - \frac{8 σ}{ρ h r^{2}} x, \end{matrix}

amiből a rezgés körfrekvenciája

\begin{matrix} ω = \sqrt[]{\frac{8 σ}{ρ h r^{2}}} = 108 s^{- 1} . \end{matrix}

C rész. I. megoldás: Abban a pillanatban, amikor a tekercseken át folyó áram maximális, a tekercseken nem esik feszültség. Emiatt a két kondenzátoron azonos nagyságú, ellentétes feszültségnek kell esnie. Jelöljük ebben a pillanatban a kondenzátorok feszültségét

U

-val, a maximális áramerősséget pedig

I_{0}

-lal.
A töltésmegmaradás miatt

q_{0} = 2 C U + C U

, amiből a kondenzátorok feszültsége

\begin{matrix} U = \frac{q_{0}}{3 C} . \end{matrix}

Az energiamegmaradás alapján

\begin{matrix} \frac{q_{0}^{2}}{4 C} = \frac{L I_{0}^{2}}{2} + \frac{2 L I_{0}^{2}}{2} + \frac{C U^{2}}{2} + \frac{2 C U^{2}}{2}, \end{matrix}

amiből pedig a maximális áram

\begin{matrix} I_{0} = \frac{q_{0}}{3 \sqrt[]{2 L C}} . \end{matrix}

Miután a

K

kapcsolót bezárjuk két, egymástól független rezgőkör alakul ki. Mindkét rezgőkör körfrekvenciája

\begin{matrix} ω = \frac{1}{\sqrt[]{2 L C}} . \end{matrix}

Az egyes rezgőkörökben a rezgés amplitúdóját, azaz az áramerősségek

{\hat{I}}_{1}

és

{\hat{I}}_{2}

maximumát az energiamegmaradás alapján határozhatjuk meg:

\begin{matrix} \frac{2 C U^{2}}{2} + \frac{L I_{0}^{2}}{2} = \frac{L {\hat{I}}_{1}^{2}}{2}, \frac{C U^{2}}{2} + \frac{2 L I_{0}^{2}}{2} = \frac{2 L {\hat{I}}_{2}^{2}}{2}, \end{matrix}

amiből

{\hat{I}}_{1} = \sqrt[]{5} I_{0}

{\hat{I}}_{2} = \sqrt[]{2} I_{0}

.
Ha az áram irányát mindkét áramkörben az óramutató járásával egyezőnek vesszük, a kapcsolón átfolyó áram:

I = I_{1} - I_{2}

, ahol az

I_{1}

és

I_{2}

áramok időfüggése:

\begin{matrix} I_{1} (t) = A cos ω t + B sin ω t, I_{2} (t) = D cos ω t + F sin ω t . \end{matrix}

A

és

D

konstansok meghatározásához írjuk fel a kezdeti feltételeket:

\begin{matrix} I_{1} (0) = A = I_{0}, I_{2} (0) = D = I_{0}, \end{matrix}

B

és

F

konstansok meghatározásához pedig a maximális áramerősségeket:

\begin{matrix} A^{2} + B^{2} = {\hat{I}}_{1}^{2}, D^{2} + F^{2} = {\hat{I}}_{2}^{2}, \end{matrix}

amiből

\begin{matrix} B = 2 I_{0}, F = - I_{0} . \end{matrix}

F

együttható negatív előjele azt fejezi ki, hogy a kapcsoló bekapcsolásának pillanatában a

2 L

induktivitású tekercs árama csökken.
Eszerint az egyes rezgőkörök áramának időfüggése:

\begin{matrix} I_{1} (t) = I_{0} (cos ω t + 2 sin ω t), I_{2} (t) = I_{0} (cos ω t - sin ω t), \end{matrix}

a kapcsolón átfolyó áram időfüggvénye pedig:

\begin{matrix} I (t) = I_{1} (t) - I_{2} (t) = 3 I_{0} sin ω t . \end{matrix}

Ebből a keresett maximális áramerősség:

\begin{matrix} I_{max} = 3 I_{0} = ω q_{0} = \frac{q_{0}}{\sqrt[]{2 L C}} . \end{matrix}

II. megoldás: Az

A

B

D

és

F

állandók meghatározása helyett a maximális áramerősséget a 2. ábrán látható vektordiagramból is meghatározhatjuk. A keresett

I_{max}

áramerősség nagyságát a

P R

szakasz hossza határozza meg.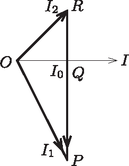

2. ábra. Vektorábra a maximális áram meghatározásához

A kapcsoló bekapcsolásakor az

I_{1}

áram növekszik, mert a

2 C

kapacitású kondenzátor továbbra is kisül, míg az

I_{2}

áram csökken, hiszen a

C

kapacitású kondenzátor tovább töltődik. Emiatt az

I_{1}

és

I_{2}

áramokat az

O P

, illetve az

O R

vektorok ábrázolják. A vektorok hossza az I. megoldás alapján

\sqrt[]{5} I_{0}

, illetve

\sqrt[]{2} I_{0}

. A kapcsoló bekapcsolásakor mindkét áram nagysága

I_{0}

, ami az ábrán éppen az

O Q

szakasz hossza.
A Pitagorasz-tétel alapján ebből:

\begin{matrix} P Q = \sqrt[]{{O P}^{2} - {O Q}^{2}} = 2 I_{0}, Q R = \sqrt[]{{O R}^{2} - {O Q}^{2}} = I_{0}, \end{matrix}

ebből pedig a keresett maximális áramerősség:

\begin{matrix} I_{max} = P R = 3 I_{0} = ω q_{0} = \frac{q_{0}}{\sqrt[]{2 L C}} . \end{matrix}

III. megoldás: Mivel a két rezgőkör körfrekvenciája megegyezik, a kapcsolón átfolyó áram körfrekvenciája is ugyanakkora lesz. A kapcsoló zárásakor a rajta átfolyó áram értéke nulla, így a kapcsolón át folyó

I

áram időfüggvénye:

\begin{matrix} I (t) = I_{max} sin ω t, ahol ω = \frac{1}{\sqrt[]{2 L C}} . \end{matrix}

Mivel a kapcsoló zárásakor ez az áram nulla

\begin{matrix} I_{max} = \frac{\dot{I}}{ω}, \end{matrix}

ahol

\dot{I}

az áram idő szerinti deriváltjának értéke a bekapcsolás pillanatában.
Legyen egy adott pillanatban a

2 C

kapacitású kondenzátor töltése

q_{1}

. Ekkor a másik kondenzátor töltése a töltésmegmaradás miatt

q_{2} = q_{0} - q_{1}

lesz. A kapcsoló zárása után

\begin{matrix} {\dot{I}}_{1} = ω^{2} q_{1}, {\dot{I}}_{2} = - ω^{2} (q_{0} - q - 1) . \end{matrix}

A kapcsolón átfolyó áram idő szerinti deriváltja

\begin{matrix} \dot{I} = {\dot{I}}_{1} - {\dot{I}}_{2} = ω^{2} q_{0}, \end{matrix}

amiből pedig a keresett maximális áram:

\begin{matrix} I_{max} = \frac{\dot{I}}{ω} = ω q_{0} = \frac{q_{0}}{\sqrt[]{2 L C}} . \end{matrix}

Ebből a megoldásból az is látszik, hogy a maximális áram értéke független a kapcsoló zárásának időpontjától.