Feladat:	4585. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Antalicz Balázs
Füzet:	2014/május, 303 - 304. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Tökéletesen rugalmas ütközések
Hivatkozás(ok):	Feladatok: 2013/december: 4585. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Megoldás. $a)$ A testek a pályájuk legalacsonyabb pontjánál, a felfüggesztés alatt fognak ütközni, hiszen az azonos hosszúságú fonálingák lengésideje független a nehezék tömegétől. Az ütközés előtt a két test sebessége ellentétes irányú és ugyanakkora, $\begin{array}{c}{\displaystyle v=\sqrt[]{2g\ell }}\end{array}$ (1) nagyságú. Ha az ütközés után a $m$ tömegú test $u$, a $M$ tömegű pedig $U$ sebességgel indul el az 1. ábrán látható irányban, akkor a lendület- és az energiamegmaradás törvénye így írható fel: 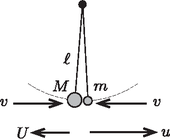${\displaystyle \begin{array}{ccc}\hfill {\displaystyle Mv-mv}& {\displaystyle =mu-MU\mathrm{,}}\hfill & \text{(<mn>2</mn>)}\\ \hfill {\displaystyle \frac{1}{2}M{v}^2+\frac{1}{2}m{v}^2}& {\displaystyle =\frac{1}{2}M{U}^2+\frac{1}{2}m{u}^2\mathrm{.}}\hfill & \text{(<mn>3</mn>)}\end{array}}$   1. ábra   A számolás egyszerűsítése érdekében célszerű bevezetni a $\begin{array}{c}{\displaystyle \frac{M}{m}=x\mathrm{,}\frac{u}{v}=y\mathrm{,}\frac{U}{v}=z}\end{array}$ dimenziótlan arányszámokat. Ezekkel ‐ némi algebrai átalakítás után ‐ (2) és (3) így írható: Ennek az egyenletrendszernek nyilvánvaló megoldása $y=z=-1$, ami annak felelne meg, hogy a két golyó ütközésmentesen mozog tovább. Ezt a lehetőséget kizárhatjuk, és eloszthatjuk $\left(3\text{'}\right)$-t $\left(2\text{'}\right)$-vel: $\begin{array}{c}{\displaystyle z-1=1-y\mathrm{.}}\end{array}$ (4) Innen $z$ kiküszöbölése után $\left(2\text{'}\right)$ felhasználásával az $u/v$ arányra $\begin{array}{c}{\displaystyle y=\frac{3x-1}{x+1}\mathrm{,}}\end{array}$ az $m$ tömegű golyó sebességére pedig az $\begin{array}{c}{\displaystyle u=\frac{3x-1}{x+1}\sqrt[]{2g\ell }=\frac{3M-m}{M+m}\sqrt[]{2g\ell }}\end{array}$ (5) érték adódik. Tételezzük fel, hogy az $m$ tömegű golyó eljut a fonál által megengedett legmagasabb pontba, ez a felfüggesztési pont felett $\ell$ magasságban található. Ebben a pontban a golyó $u\text{'}$ sebességére (az energiamegmaradás tétele szerint) fennáll: $\begin{array}{c}{\displaystyle \frac{1}{2}m{u}^2=\frac{1}{2}mu{\text{'}}^2+2g\ell \mathrm{,}}\end{array}$ tehát   $\begin{array}{c}{\displaystyle u\text{'}=\sqrt[]{u^2-4g\ell }\mathrm{.}}\end{array}$ (6) Ha $u\text{'}$ nem elég nagy, akkor a fonál meglazul, és a golyó nem jut el a legfelső pontba. A pálya legfelső pontjában (lásd a 2. ábrát) a fonalat feszítő erő (Newton mozgásegyenlete szerint) 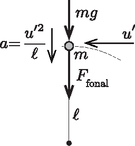$\begin{array}{c}{\displaystyle F_{\text{fonal}}=m\frac{u{\text{'}}^2}{\ell }-mg\ge 0.}\end{array}$ (7)   2. ábra   (Belátható, hogy (7) teljesülése esetén a pálya minden pontjában feszes marad a fonal.) A (7) egyenlőtlenséget (6)-ba helyettesítve az $u^2>5g\ell$ megszorítást kapjuk, amit (5)-tel összevetve a keresett tömegarányra végül az $\begin{array}{c}{\displaystyle x=\frac{M}{m}\ge \frac{\sqrt[]{2}+\sqrt[]{5}}{3\sqrt[]{2}-\sqrt[]{5}}\approx 1\mathrm{,}82}\end{array}$ korlátot kapjuk. $b)$ Vizsgáljuk meg, milyen magasra jut el a $M$ tömegű test, ha a tömegek aránya éppen a kritikus érték! Az (5) összefüggésből kiszámíthatjuk, hogy $y=1\mathrm{,}58$, (4)-ből pedig a $M$ tömegű test ütközés utáni sebességét: $\begin{array}{c}{\displaystyle z=2-y=0\mathrm{,}42;U=0\mathrm{,}42\sqrt[]{2g\ell }\mathrm{.}}\end{array}$ (Mivel $U>\mathrm{0,}$ a test ténylegesen az 1. ábrán látható irányban, ,,visszafelé'' mozog az ütközés után.) A test további mozgására felírható az energiamegmaradás törvénye: $\begin{array}{c}{\displaystyle \frac{m{U}^2}{2}=mgh\mathrm{,}}\end{array}$ ahonnan az emelkedés magassága: $\begin{array}{c}{\displaystyle h=\frac{U^2}{2g}=0\mathrm{,}175\ell \mathrm{,}}\end{array}$ ami a 3. ábrán látható emelkedési szöget is meghatározza: 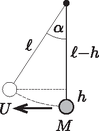$\begin{array}{c}{\displaystyle \alpha =\text{arccos}\frac{\ell -h}{\ell }\approx 34\mathrm{,}{4}^{\circ }\mathrm{.}}\end{array}$   3. ábra