Kezdőlap


Feladat:	4593. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Balogh Menyhért , Gnädig Péter , Horicsányi Attila
Füzet:	2014/március, 182 - 185. oldal		PDF \| MathML
Témakör(ök):	Feladat, Egyéb részecskefizika, Relativisztikus impulzus, Relativisztikus energia
Hivatkozás(ok):	Feladatok: 2013/december: 4593. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Rugalmas ütközésénél a részecskék összenergiája is és a lendületük (impulzusuk) vektori összege is változatlan marad. Ezeket a mennyiségeket a fénysebességet megközelítő sebességeknél a relativisztikus mechanika törvényei szerint számíthatjuk ki.
Egy $m$ nyugalmi tömegű, $v$ sebességű részecske (teljes) energiája

\begin{matrix} E = \frac{m c^{2}}{\sqrt[]{1 - \frac{v^{2}}{c^{2}}}}, \end{matrix}

(1)

impulzusa pedig

\begin{matrix} p = \frac{m v}{\sqrt[]{1 - \frac{v^{2}}{c^{2}}}}, \end{matrix}

(2)

ami

\begin{matrix} p = \frac{E}{c^{2}} v \end{matrix}

(3)

alakban is felírható. Ultrarelativisztikus határesetben (vagyis amikor

| b o l d s y m b o l v | = v \approx c

) az energia és az impulzus nagyságának kapcsolata:

\begin{matrix} E \approx p c . \end{matrix}

(4)

Ugyanez az összefüggés az (1) és (2)-ből a sebesség kiküszöbölése után közvetlenül adódó

E^{2} = {(p c)}^{2} + {(m c^{2})}^{2}

relációból is leolvasható, ha abban ‐ ultrarelativisztikus határesetben ‐ az

m c^{2}

nyugalmi energiát a részecske teljes

E

energiája mellett elhanyagoljuk.

Jelöljük a feladatunkban szereplő részecskék ütközés utáni lendületét

q_{1}

-gyel és

q_{2}

-vel. Feltételezve, hogy ezek is ultrarelativisztikus impulzusok, a megmaradási törvények így írhatók fel:

\begin{matrix} p_{1} + p_{2} = q_{1} + q_{2}, \end{matrix}

(5)

illetve

p_{1} c + p_{2} c = q_{1} c + q_{2} c

, vagyis

\begin{matrix} p_{1} + p_{2} = q_{1} + q_{2} . \end{matrix}

(6)

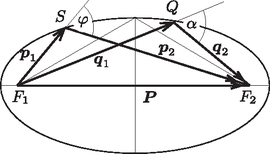1. ábra

A fenti egyenleteket az 1. ábrán látható módon szemléltethetjük. A részecskék adott

p_{1}

és

p_{2}

impulzusából megszerkeszthető a

P = p_{1} + p_{2}

összimpulzus vektora, amely egyúttal az ütközés utáni impulzusok összege. Az energiamegmaradás (6) képlete szerint a még ismeretlen

Q

pontnak a

P

vektor végpontjaitól mért távolság-összege egy ismert nagyságú távolság:

\begin{matrix} q_{1} + q_{2} = F_{1} Q + F_{2} Q = állandó (= p_{1} + p_{2}) . \end{matrix}

(7)

A (7) egyenlet szerint a

Q

pont egy olyan ellipszisre illeszkedik, amelynek fókuszpontjai

F_{1}

és

F_{2}

, nagytengelye pedig az ismert (és megszerkeszthető)

p_{1} + p_{2}

távolság.
Kérdés: Az ellipszis melyik pontjánál lesz a szétrepülő részecskék mozgásiránya, vagyis az ábrán látható

α

szög a legkisebb? Belátjuk, hogy

α

akkor minimális, amikor

Q

az ellipszis kistengelyének valamelyik végpontja, vagyis amikor

q_{1} = q_{2}

. Írjuk fel az

F_{1} S F_{2}

és az

F_{1} Q F_{2}

háromszögekre a koszinusztételt:

\begin{matrix} p_{1}^{2} + p_{2}^{2} + 2 p_{1} p_{2} cos φ = P^{2} = q_{1}^{2} + q_{2}^{2} + 2 q_{1} q_{2} cos α, \end{matrix}

(8)

illetve képezzük a (6) egyenlet mindkét oldalának négyzetét:

\begin{matrix} p_{1}^{2} + p_{2}^{2} + 2 p_{1} p_{2} = q_{1}^{2} + q_{2}^{2} + 2 q_{1} q_{2} . \end{matrix}

(9)

Vonjuk ki (9)-ből (8)-at:

2 p_{1} p_{2} (1 - cos φ) = 2 q_{1} q_{2} (1 - cos α)

, ahonnan a kérdéses szög koszinusza kifejezhető:

\begin{matrix} cos α = 1 - \frac{p_{1} p_{2} (1 - cos φ)}{q_{1} q_{2}} . \end{matrix}

Látható, hogy

α

akkor a legkisebb, amikor a

q_{1} q_{2}

szorzat a legnagyobb, hiszen a többi kifejezés a

Q

pont helyzetétől független. De mivel

q_{1} + q_{2}

adott érték, a számtani és mértani közepekre vonatkozó egyenlőtlenség szerint

\begin{matrix} q_{1} q_{2} \leq {(\frac{q_{1} + q_{2}}{2})}^{2} = {(\frac{p_{1} + p_{2}}{2})}^{2}, \end{matrix}

és az egyenlőség akkor teljesül, ha

q_{1} = q_{2}

.
A fenti eredmények ismeretében az

α

szöget a következőképpen szerkeszthetjük meg:
1. Az egyik vektor párhuzamos eltolásával (az 1. ábrán látható módon) megszerkesztjük a

p_{1}

és

p_{2}

vektorok összegét,

P

-t.
2. Egy egyenesre felmérjük

p_{1}

-et és

p_{2}

-t, majd a

p_{1} + p_{2}

hosszúságú szakaszt elfelezzük (2. ábra).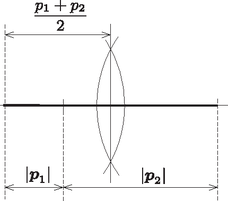

2. ábra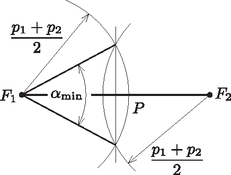

3. ábra

3. Megrajzoljuk azt a két kört, amelyek sugara

\frac{p_{1} + p_{2}}{2}

, középpontjuk pedig

P

kezdő-, illetve végpontja. A körök metszéspontjai kitűzik

q_{1}

és

q_{2}

irányát, és megadják a legkisebb szétrepülési szög nagyságát (3. ábra).
Hátra van még annak igazolása, hogy az ultrarelativisztikus részecskék az ütközés után is a fénysebességhez közeli sebességekkel mozognak, tehát a fenti megoldásban alkalmazott ultrarelativisztikus energiaképlet jogos közelítés. Tételezzük fel ennek ellenkezőjét, vagyis azt, hogy az egyik részecske az ütközés után nagyon lassan mozog. (Mindkettő nyilván nem lassulhat le, hiszen az összes energia sokkal nagyobb, mint a részecskék nyugalmi energiája.) Ha ez következne be, akkor az energia- és a lendületmegmaradás képlete így nézne ki:

\begin{matrix} p_{1} c + p_{2} c \approx q_{1} c, p_{1} + p_{2} \approx q_{1}, \end{matrix}

mert a ,,lassú'' részecske energiája is és a lendülete is elhanyagolható a másik (gyors) részecske megfelelő adatai mellett. Ez azonban nem lehetséges, a fenti két egyenlet egymásnak ellentmond, hiszen a háromszög-egyenlőtlenség szerint

\begin{matrix} q_{1} = | p_{1} + p_{2} | \leq | p_{1} | + | p_{2} |, tehát p_{1} c + p_{2} c > q_{1} c . \end{matrix}

(Az egyenlőség csak akkor állhatna fenn, ha

p_{1}

és

p_{2}

párhuzamosak lennének, ez pedig ‐ a megadott rajz szerint ‐ nem teljesül.)

Megjegyzések. 1. A megoldás során sehol nem kapott szerepet a részecskék nyugalmi tömege, az (ultrarelativisztikus közelítésben) meg se jelent a képletekben. Emiatt a levont következtetés akkor is érvényben marad, ha az ütközés után nem az eredeti részecskék, hanem azoknál nagyobb (vagy kisebb) nyugalmi tömegű részecskepár repül szét. Ilyen folyamat valóban megfigyelhető a Természetben; példa erre az

\begin{matrix} e^{+} + e^{-} \to μ^{+} + μ^{-} \end{matrix}

ütközés. (

μ

az elektronnál kb. 200-szor nagyobb tömegű, müon nevű részecskét jelöli,

e^{+}

pedig a pozitron jele.)
2. A szétrepülő részecskék szögének legnagyobb értéke akár

180^{\circ}

is lehet, tehát egymással ellentétes irányban is mozoghatnak.

(G. P.)