Kezdőlap


Feladat:	330. fizika mérési feladat	Korcsoport: 14-15	Nehézségi fok: nehéz
Megoldó(k):	Agócs Fruzsina , Horicsányi Attila , Kollarics Sándor , Olosz Balázs , Szabó Attila
Füzet:	2014/január, 46 - 49. oldal		PDF \| MathML
Témakör(ök):	Mérési feladat, Mechanikai mérés
Hivatkozás(ok):	Feladatok: 2013/február: 330. fizika mérési feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. A mérés eszközei:
‐ kb. 3 cm vastag habszivacs (kb.

30 \times 30

cm-es) és hasonló méretű deszkalap,
‐ laminált padló (kb.

20 \times 120

cm-es),
‐ léc (kb. 150 cm-es),
‐ csapágygolyók (3,1 és 19 mm közti átmérőjűek),
‐ tolómérő, szögmérős vízmérték,
‐ könyvek és cipősdoboz alátámasztásnak.

A mérési elrendezés. A habszivacsot a deszkára helyeztem, majd a deszka egyik végét könyvek segítségével felpolcoltam, ezt a véget gyurmával rögzítettem. A másik véghez a laminált padlóból készített lejtőt illesztettem: két kupac alátámasztáson végigfektettem a lécet, majd rátettem a padlót úgy, hogy az egyik vége szorosan illeszkedjen a habszivacshoz (a lécre azért volt szükség, mert a padló önmagában nem elég erős, behajlott volna az alátámasztások közt). Az illeszkedés törésmentessé tételére egy kis darab vastagabb fénymásolópapírt helyeztem a találkozási felületre: ez simán felfeküdt mindkét oldalon és az illeszkedést ívesen, törés nélkül áthidalta. A kész elrendezés a fényképen látható.

Otthon nagy mennyiségű csapágygolyó állt rendelkezésre, ezeket tolómérő segítségével osztályoztam: 15-féle átmérőjű golyót találtam, 3,1 és 19,0 mm közti átmérővel (ezek hibája 0,05 mm, ami elhanyagolható). Először megmértem mindkét lejtő hajlásszögét: ehhez szögmérővel ellátott, állítható vízmértéket használtam. A padlóból készült lejtő hajlásszöge végig

α = {(6 \pm 0, 2)}^{\circ}

volt, a szivacsból készült lejtőt két állásban is használtam, ezek hajlásszöge rendre

β_{1} = {(17 \pm 0, 2)}^{\circ}

és

β_{2} = {(22 \pm 0, 2)}^{\circ}

volt. Ezután a padlólapot beskáláztam, illetve a habszivacson is megjelöltem egy pontot, ahonnan a golyókat indítottam. A skála kezdőpontjának és a habszivacson megjelölt pontnak a távolságát a két lejtő síkjának metszésvonalától rendre

x_{0} = (10, 0 \pm 0, 1)

és

x_{1} = (30, 0 \pm 0,3)

cm-nek állítottam be. Az áthidaló papírt úgy helyeztem a habszivacsra, hogy a kijelölt ponttól

ℓ = (28, 0 \pm \pm 0, 1)

cm-re legyen: a vizsgált mechanikai energiaveszteség csak ezen a szakaszon lép fel.

A mérés elve és menete. A golyót a habszivacson elhelyezett jelöléshez állítottam és hagytam legurulni. A szivacsról a padlólapra átgurulva, a golyó további energiavesztesége elhanyagolhatóan kicsi (egy ilyen típusú padlóval lerakott szoba egyik végéből egy golyó észrevehető lassulás nélkül képes volt átgurulni a másikba, még igen kis kezdősebességnél is), tehát az a magasság, ameddig a golyó fel tud jutni, egyértelműen megadja a megmaradt mozgási energia mértékét, amiből az energiaveszteség mértéke is kiszámítható. A mérés során tehát elegendő azt az

L

távolságot megmérni, ameddig a legurított golyó feljut a másik lejtőn: ezt a lejtőre rajzolt skála segítségével centiméteres pontossággal le lehet olvasni. A golyó pályája a habszivacs kisebb-nagyobb egyenetlenségei miatt gyakran eltérült, így a golyó lefutott a padlóról: ezeket nem vettem figyelembe a mérésnél. Minden golyóátmérővel 10-10 mérést végeztem a lejtő mindkét állása mellett, ezeknek átlaga és szórása is szerepel a táblázatban. (A táblázatokat terjedelmi okokból nem közöljük. A Szerk.)

A mért adatok feldolgozása. Mechanikai energiaveszteségnek az indítási pont és a szivacsos szakasz vége közti helyzeti energia csökkenés, valamint a leérkező golyó mozgási energiája közti különbséget nevezzük. Az energiaveszteségnek a kezdeti mechanikai energiához viszonyított arányát

λ

-val jelöltem, a feladat éppen ennek az arányszámnak a mérése.
Vegyük fel a helyzeti energia nullaszintjét a két sík metszésvonalában: ekkor a golyó helyzeti energiája kezdetben

E_{h 0} = m g h_{1} = g x_{1} sin β

, a szivacsról való lefutás pillanatában

\begin{matrix} E_{h 2} = m g h_{2} = m g (x_{1} - ℓ) sin β . \end{matrix}

A felszabaduló helyzeti energia

Δ E_{h} = m g ℓ sin β

. A mechanikai energiaveszteség definíciója szerint ebben a pillanatban a golyó mozgási energiája

K = (1 - λ ℓ) m g sin β

, a teljes mechanikai energia tehát

\begin{matrix} E_{mech} = m g (x_{1} - λ ℓ) sin β . \end{matrix}

Mivel a padlólapon a mechanikai energiaveszteség elhanyagolható, a lejtő tetején, a fordulópontnál is ennyi a golyó mechanikai energiája. Ez a két lejtő metszésvonalától

L + x_{0}

távolságra van, így a fordulópontnál a helyzeti energia (mozgási energia nincs):

\begin{matrix} E_{mech} = m g (L + x_{0}) sin α . \end{matrix}

A mechanikai energia két kifejezése egyenlő:

\begin{matrix} m g (x_{1} - λ ℓ) sin β = m g (L + x_{0}) sin α, \end{matrix}

ahonnan az energiaveszteség mértéke:

\begin{matrix} λ = \frac{x_{1}}{ℓ} - \frac{L + x_{0}}{ℓ} \cdot \frac{sin α}{sin β} . \end{matrix}

λ

kiszámított numerikus értékeit a mért adatok táblázatában adtam meg. A két hajlásszög-értékre grafikusan ábrázoltam a

λ (r)

értékpárokat, ezek láthatók az 1. ábrán és a 2. ábrán.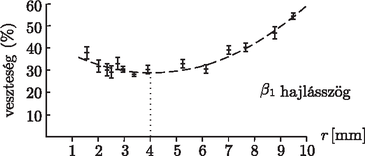

1. ábra. A mechanikai energiaveszteség relatív mértéke a golyó sugarának függvényében ,,laposabb'' lejtőn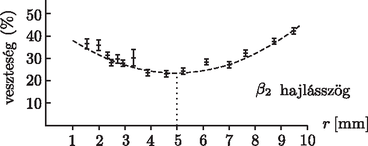

2. ábra. A mechanikai energiaveszteség relatív mértéke a golyó sugarának függvényében ,,meredekebb'' lejtőn

Mindkét esetben látható, hogy

λ (r)

kis

r

-ekre csökken, majd egy minimum elérése után növekedni kezd. Ezt a gördülési ellenállást okozó két fő tényezővel magyarázhatjuk. A kis átmérőjű golyókat a habszivacs ,,durva'' felszíne (mm nagyságrendű buborékokból álló anyagról van szó) akadályozza a mozgásban: egyik buborékból a másikba átjutásuk igényel folyamatos energiabefektetést. Ez a fajta energiaveszteség nyilván csökken a golyó átmérőjének növekedtével, hiszen a leküzdendő akadályok mérete elhanyagolhatóvá válik a golyó méretéhez képest. A nagyobb átmérőjű golyókat más hatás fékezi: ezek a rugalmas szivacsot észrevehetően benyomják, amely a golyó továbbgurulta után nem áll vissza azonnal, az átmenetileg ,,benn maradó'' rugalmas energiát a golyó már nem tudja felvenni. Ez a hatás a benyomódás mértékével, azaz a golyó tömegével nő. A két hatás együttese alakítja ki a minimumhelyes függvényt.
Mivel a függvény alakjának elméleti meghatározása bonyolult feladat lenne, a minimum helyének megbecslésére másofokú függvényt illesztettem mindkét grafikonra, amelyek a felvett pontokat elég jól lefedik. A minimum helye

β_{1}

meredekségű lejtőn

r_{1} = (4, 1 \pm 0, 3) mm\approx4 mm

, a

β_{2}

állású lejtőn

r_{2} = (5, 0 \pm 0, 3) mm\approx5 mm

. (A szélsőérték helyét a mérés pontatlansága és a másodfokú függvény használatának elméleti megalapozatlansága miatt nem érdemes mm-nél pontosabban megadni). Meglepő azonban, hogy a minimum helye a mérési hibán jóval kívül esően eltér a két esetben; ennek elméleti magyarázata talán az lehet, hogy a benyomódás mértéke a meredekebb lejtőn kisebb, ezért a nagy átmérőjű golyókat fékező hatás gyengébb, miközben a kis átmérőjű golyók ugyanannyira fékeződnek.