Kezdőlap


Feladat:	4528. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Gnädig Péter , Olosz Balázs
Füzet:	2013/szeptember, 369 - 371. oldal		PDF \| MathML
Témakör(ök):	Feladatok, Kötelek (láncok) egyensúlya
Hivatkozás(ok):	Feladatok: 2013/március: 4528. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a kötél egységnyi hosszúságú darabjának tömegét

m^{*}

-gal, a függőlegesen lelógó egy-egy rész hosszát pedig

x

-szel (1. ábra)!
Vizsgáljuk a belógó kötél egyik felének egyensúlyát (2. ábra)! Ennek a résznek a súlya

m^{*} g ℓ / 2

. A kötelet feszítő erő vízszintes

F

komponense a kötél minden pontjában ugyanakkora, hiszen a nehézségi erő függőleges. A függőleges komponens helyről helyre változik, a kötél közepénél nulla, a szegnél pedig a belógó rész felének súlya: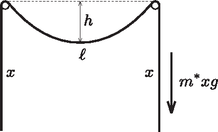

m^{*} \frac{ℓ}{2} g

1. ábra

A szegnél ható erő nagysága, ami a lelógó függőleges kötél súlyával egyenlő, Pitagorasz tétele alapján számítható:

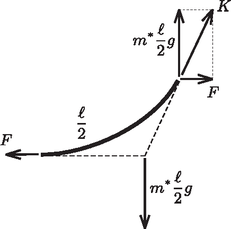\begin{matrix} K = \sqrt[]{{(m^{*} \frac{ℓ}{2} g)}^{2} + F^{2}} = m^{*} x g . \end{matrix}

(1)

2. ábra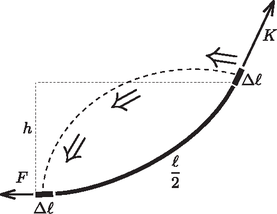

3. ábra

Képzeljük el, hogy a kötelet a belógó rész közepénél elvágjuk, majd egy kicsiny,

Δ ℓ

hosszúságú darabbal nagyon lassan feljebb húzzuk, végül pedig a szegnél a

Δ ℓ

hosszúságú darabot kivágjuk és visszavisszük az elvágás helyére, majd ott visszatoldjuk a kötélbe (3. ábra). Mivel ilymódon az eredeti állapothoz jutunk vissza, az összes munkavégzés nulla kell legyen:

W = K Δ ℓ - F Δ ℓ - m^{*} Δ ℓ g h = 0

, vagyis

\begin{matrix} K = F + m^{*} g h . \end{matrix}

(2)

(1) és (2) összevetéséből a függőlegesen lelógó részek hosszára

\begin{matrix} x = \frac{ℓ^{2}}{8 h} + \frac{h}{2}, \end{matrix}

a kötél keresett teljes hosszára pedig

\begin{matrix} L = 2 x + ℓ = \frac{ℓ^{2}}{4 h} + h + ℓ \end{matrix}

adódik, amit

\begin{matrix} L = \frac{{(2 h + ℓ)}^{2}}{4 h} \end{matrix}

alakban is fel lehet írni.

II. megoldás. Osszuk fel a kötelet (gondolatban) kicsiny,

Δ s_{i}

hosszúságú darabkákra

(i = 1,2, ..., N)

, és jelöljük a kis darabkák végpontjai közötti magasságkülönbséget

Δ y_{i}

-vel (4. ábra). Ha

G_{i}

i

-edik kis darabka egyik végpontjánál ható függőleges irányú erő,

F

pedig az

i

-től független vízszintes erőkomponens, akkor az eredő

K_{i}

nagyságára fennáll:

\begin{matrix} G_{i}^{2} + F^{2} = K_{i}^{2} . \end{matrix}

(3)

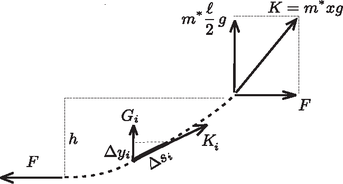4. ábra

Fennáll továbbá, hogy

\begin{matrix} G_{i + 1} - G_{i} \equiv Δ G_{i} = m^{*} Δ s_{i} g, \end{matrix}

ahol

m^{*}

a kötél egységnyi hosszának tömege, valamint a kötéldarabkákra ható erő és az érintő megegyező irányából:

\begin{matrix} Δ y_{i} = Δ s_{i} \frac{G_{i}}{K_{i}} = \frac{1}{m^{*} g} \frac{G_{i} Δ G_{i}}{K_{i}} = \frac{1}{2 m^{*} g} \frac{Δ (G_{i}^{2})}{K_{i}} . \end{matrix}

(4)

Az utolsó lépésnél kihasználtuk, hogy bármilyen

f

mennyiség négyzetének kicsiny megváltozása:

\begin{matrix} Δ f^{2} \equiv {(f + Δ f)}^{2} - f^{2} = 2 f Δ f + {(Δ f)}^{2} \approx 2 f Δ f, \end{matrix}

(5)

Δ f ≪ f

.
Képezzük a (3) egyenlet mindkét oldalának kicsiny megváltozását, vagyis hasonlítsuk össze az

(i + 1)

-edik és az

i

-edik egyenletet, és alkalmazzuk az (5) azonosságot! Mivel

F

i

-től független állandó,

\begin{matrix} G_{i} Δ G_{i} = K_{i} Δ K_{i}, \end{matrix}

azaz (4) így írható:

\begin{matrix} Δ y_{i} = \frac{1}{m^{*} g} \frac{G_{i} Δ G_{i}}{K_{i}} = \frac{1}{m^{*} g} \frac{K_{i} Δ K_{i}}{K_{i}} = \frac{1}{m^{*} g} Δ K_{i} . \end{matrix}

Összegezzük a fenti egyenletben szereplő

Δ y_{i}

mennyiségeket a kötél belógó részének felére. Mivel

\sum Δ y = h

, a 4. ábra jelöléseivel

\begin{matrix} h = \frac{1}{m^{*} g} (K - F) . \end{matrix}

Ez éppen az I. megoldás (2) egyenlete, amelyből (1) felhasználásával a kötél teljes hosszára az

\begin{matrix} L = \frac{{(2 h + ℓ)}^{2}}{4 h} \end{matrix}

eredmény adódik.