Kezdőlap


Feladat:	4507. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Antalicz Balázs , Balogh Menyhért , Csáky Pál , Kovács Áron , Novák László , Olexo Tünde , Sal Kristóf , Sárvári Péter , Szabó Attila , Ürge László
Füzet:	2013/április, 242 - 245. oldal		PDF \| MathML
Témakör(ök):	Feladat, Tökéletesen rugalmas ütközések
Hivatkozás(ok):	Feladatok: 2013/január: 4507. fizika feladat

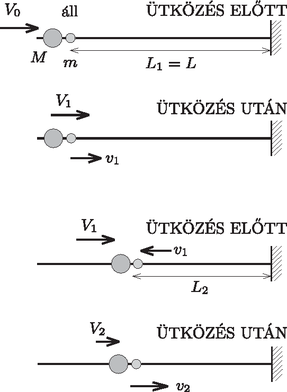
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a $M$ tömegű golyó $n$ -edik ütközés utáni sebességét $V_{n}$ -nel, a $m$ tömegű golyó sebességét $v_{n}$ -nel, az $n$ -edik ütközés helye és a fal közötti távolságot pedig $L_{n}$ -nel! (Az első 2 ütközés hely- és sebességadatait az ábra mutatja.

A két golyó ütközéseire nyilván érvényes a lendület és a mechanikai energia megmaradásának törvénye. Írjuk fel ezeket a megmaradási törvényeket az

(n + 1)

-edik ütközésre:

\begin{matrix} \frac{1}{2} M (V_{n}^{2} - V_{n + 1}^{2}) = \frac{1}{2} m (v_{n + 1}^{2} - v_{n}^{2}), \end{matrix}

(1)

\begin{matrix} M (V_{n} - V_{n + 1}) = m (v_{n + 1} + v_{n}) . \end{matrix}

(2)

A fenti két egyenletet egymással elosztva kapjuk:

\begin{matrix} V_{n} + V_{n + 1} = v_{n + 1} - v_{n}, \end{matrix}

vagyis

\begin{matrix} V_{n} + v_{n} = v_{n + 1} - V_{n + 1} . \end{matrix}

(3)

Az ábrán szereplő két ütközés között a

M

tömegű test

V_{1}

sebességgel

L_{1} - L_{2}

utat, a

m

tömegű test pedig

v_{1}

sebességgel

L_{1} + L_{2}

utat tesz meg ugyanannyi idő alatt:

\begin{matrix} \frac{L_{1} - L_{2}}{V_{1}} = \frac{L_{1} + L_{2}}{v_{1}}, \end{matrix}

innen következik, hogy

\begin{matrix} L_{2} = L_{1} \frac{v_{1} - V_{1}}{v_{1} + V_{1}} . \end{matrix}

Hasonló módon számítható az

(n - 1)

-edik és az

n

-edik ütközés között eltelt idő:

\begin{matrix} \frac{L_{n - 1} - L_{n}}{V_{n - 1}} = \frac{L_{n - 1} + L_{n}}{v_{n - 1}}, \end{matrix}

ahonnan

\begin{matrix} L_{n} = L_{n - 1} \frac{v_{n - 1} - V_{n - 1}}{v_{n - 1} + V_{n - 1}} . \end{matrix}

(4)

A (3) összefüggés szerint (4) nevezőjében

v_{n - 1} + V_{n - 1}

helyébe

v_{n} - V_{n}

írható, vagyis fennáll:

\begin{matrix} L_{n} (v_{n} - V_{n}) = L_{n - 1} (v_{n - 1} - V_{n - 1}) . \end{matrix}

(5)

Találtunk tehát egy olyan mennyiséget, az

L_{k} (v_{k} - V_{k})

kifejezést, amely minden

k

-ra ugyanakkora, így a legelső és a falhoz legközelebb történő

N

-edik ütközésre is megegyezik:

\begin{matrix} L_{N} = L_{1} \frac{v_{1} - V_{1}}{v_{N} - V_{N}} . \end{matrix}

(6)

Az első ütközés helye a faltól

L_{1} = L

távolságra történik, továbbá a (3) egyenlet alapján

v_{1} - V_{1} = v_{0} + V_{0} = V_{0}

(hiszen kezdetben a

m

tömegű golyó nyugalomban volt, azaz

v_{0} = 0

). Ezek szerint

\begin{matrix} L_{N} = L \frac{V_{0}}{v_{N} - V_{N}} . \end{matrix}

(7)

Tegyük fel, hogy a

M

tömegű golyó sebessége az

N

-edik ütközés után éppen nullára csökken,

V_{N} = 0

lesz. (Ha nem is állna meg teljesen a

M

tömegű golyó, de a következő ütközés után már ,,visszafele'' haladna, akkor is jó közelítéssel nullának vehető a sebessége, hiszen az

M ≫ m

feltétel azt jelenti, hogy a nagyobb tömegű golyó csak nagyon kis adagokban veszíti el a sebességét.)
Mivel a nagyobb golyó sebessége nulla, ezért a teljes kezdeti mozgási energiát már átadta a kis golyónak:

\begin{matrix} \frac{1}{2} M V_{0}^{2} = \frac{1}{2} m v_{N}^{2}, ahonnan v_{N} = V_{0} \sqrt[]{\frac{M}{m}} . \end{matrix}

Visszahelyettesítve (7)-be és

V_{N} = 0

-t is kihasználva végül a keresett távolságra az

\begin{matrix} L_{{min}_{}^{}} = L \sqrt[]{\frac{m}{M}} \end{matrix}

eredményt kapjuk.

II. megoldás. Az I. megoldás jelöléseit követjük. Az energia- és a lendületmegmaradás törvényéből következik, hogy a

m

tömegű golyó az első ütközés után

\begin{matrix} v_{1} = \frac{2 V_{0}}{1 + \frac{m}{M}} \approx 2 V_{0} \end{matrix}

sebességgel kezd mozogni, tehát a mozgási energiája

\begin{matrix} E_{1} = \frac{1}{2} m v_{1}^{2} \approx 2 m V_{0}^{2} . \end{matrix}

Ezek után úgy is felfoghatjuk az eseményeket, mintha a nagy golyó egy kis (kezdetben

A L

térfogatú) csőben adiabatikusan összenyomna egy olyan gázt, amelynek belső energiája a kis golyó mozgási energiája, azaz kezdetben

E_{1}

, és szabadsági foka 1 (mivel a ,,gázrészecske'' csak egyetlen dimenzióban, a vízszintes rúd irányába mozdulhat el). A cső

A

keresztmetszetét önkényesen választhatjuk, nagysága a továbbiak szempontjából lényegtelen.

Megjegyzés. Ez a leírás nem teljesen pontos, hiszen a szokásos esettel ellentétben itt most egyetlen részecske alkotja a ,,gázt'', és emiatt a ,,dugattyú'' (vagyis a

M

tömegű test) nem folyamatosan, hanem lökésszerűen fejt ki erőt a másik testre. Igaz ugyan, hogy ezek az erőlökések csak kezdetben ritkák, a kis test sebességének növekedtével egyre jobban összesűrűsödnek, majdnem folytonossá válnak. Az egyetlen részecske problémát még kikerülhetjük, ha nagyon nagy számú vízszintes rudat képzelünk el, mindegyiken egy-egy

m

tömegű, kezdetben álló golyó, s ezeknek ütközik egyetlen, nagy tömegű ,,dugattyú''. Ez a kép már jobban emlékeztet a kinetikus gázelmélet leírásmódjára, de a dugattyú kezdetben lökésszerű erőkifejtését nem oldja meg.
A leírtak miatt a ,,gázmodell'' alapján számított eredményt nem fogjuk számszerűen pontosnak tekinteni, inkább csak nagyságrendi becslésként értelmezhetjük.

Adiabatikus állapotváltozás esetén

\begin{matrix} p_{1} V_{1}^{κ} = p_{2} V_{2}^{κ}, \end{matrix}

(8)

ahol

κ = (f + 2) / f

, jelen esetben

f = 1

miatt

κ = 3

. A gáz belső energiája

\begin{matrix} = \frac{f}{2} N k T = \frac{1}{2} p V, \end{matrix}

vagyis a kezdeti és a (legjobban összenyomott) végállapotra felírva:

\begin{matrix} \frac{E_{1}}{E_{2}} = \frac{p_{1} V_{1}}{p_{2} V_{2}} . \end{matrix}

Ez az arány (8) felhasználásával így is írható:

\begin{matrix} \frac{E_{1}}{E_{2}} = \frac{V_{1}^{1 - κ}}{V_{2}^{1 - κ}} = \frac{V_{2}^{2}}{V_{1}^{2}} = {(\frac{L_{2}}{L_{1}})}^{2} . \end{matrix}

A kezdeti állapotban

L_{1} = L

és

E_{1} = 2 m V_{0}^{2}

, a végállapotban pedig

L_{2} = L_{min}

a keresett megközelítési távolság. Tudjuk még, hogy a 2-es állapotban a ,,gáz'' energiája

E_{2} = \frac{1}{2} M V_{0}^{2}

, hiszen a ,,dugattyú'' sebessége a falhoz legközelebbi helyzetben pontosan (vagy jó közelítéssel) nulla, így a rendszer teljes mechanikai energiája a ,,gázrészecskére'' jut.
Ezek szerint a keresett távolságra fennáll:

\begin{matrix} \frac{L_{min}}{L} = \sqrt[]{\frac{E_{1}}{E_{2}}} = \sqrt[]{\frac{2 m V_{0}^{2}}{\frac{1}{2} M V_{0}^{2}}} = 2 \sqrt[]{\frac{m}{M}} . \end{matrix}

Ez az eredmény egy 2-es faktorban tér el az I. megoldás ,,pontos'' végeredményétől, de ez az eltérés ‐ az említett okok miatt ‐ érthető.

Megjegyzés. A golyók sebessége helyett bevezethetjük az

x_{i} = \sqrt[]{M} V_{i}

és

y_{i} = \sqrt[]{m} v_{i}

új változókat. Ezekkel kifejezve az energiamegmaradás törvénye így írható fel:

x_{i}^{2} + y_{i}^{2} = állandó

, vagyis az ütközések során az átskálázott sebességkoordináták

x - y

síkján egy kör mentén mozog a rendszer. Belátható, hogy minden egyes ütközésnél

\begin{matrix} φ = arctg \sqrt[]{m / M} \approx \sqrt[]{m / M} \end{matrix}

szöggel kell odébblépnünk ezen a körön, összesen tehát (egy negyedkörnyi elfordulás után)

\begin{matrix} N = \frac{π}{4} \sqrt[]{\frac{M}{m}} ≫ 1 \end{matrix}

számú ütközés zajlik le, amíg a

M

tömegű golyó legjobban megközelíti a falat.