Feladat:	2012. évi Nemzetközi Fizika Diákolimpia 1. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Sarlós Ferenc ,  Vankó Péter ,  Vigh Máté
Füzet:	2012/november, 489 - 493. oldal		PDF  |  MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia, Egyéb feladatok
Hivatkozás(ok):	Feladatok: 2012/október: 2012. évi Nemzetközi Fizika Diákolimpia 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.     1. feladat. Ragadd meg a lényeget! A rész. Hajítás. i.   Ha a golyót függőlegesen felfelé dobjuk, akkor ‐ a mechanikai energia megmaradása   alapján ‐ eléri az $x=0$, $z=\frac{v_0^2}{2g}$ pontot. Ezt összehasonlítva a $z\le z_0-k{x}^2$ egyenlőtlenséggel $\begin{array}{c}{\displaystyle z_0=\frac{v_0^2}{2g}}\end{array}$ adódik. A $k$ állandó meghatározásához vizsgáljuk a $z\to -\infty$ határesetet! Ebben a határesetben a golyó akkor jut (adott $z$ érték esetén) vízszintes irányban a legmesszebbre, ha a parabolapálya a leglaposabb, azaz ha a golyót vízszintesen hajítjuk el. Ekkor $\begin{array}{c}{\displaystyle z=-\frac{g}{2v_0^2}{x}^2\mathrm{.}}\end{array}$ Ezt beírva a megadott, most $x\to \infty$ határesetben vizsgált egyenlőtlenségbe $\begin{array}{c}{\displaystyle -\frac{g}{2v_0^2}{x}^2\le z_0-k{x}^2\mathrm{,}\text{azaz}k-\frac{g}{2v_0^2}\le \frac{z_0}{x^2}\to 0.}\end{array}$ Innen $k\le \frac{g}{2v_0^2}$. Ha $k<\frac{g}{2v_0^2}$ teljesülne, akkor (nagy $x$-re) a golyó által elérhető tartomány és a megadott egyenlőtlenség által meghatározott tartomány között egy ,,rés'' lenne, ezt a lehetőséget tehát kizárhatjuk. Eszerint a kérdezett paraméter: $\begin{array}{c}{\displaystyle k=\frac{g}{2v_0^2}\mathrm{.}}\end{array}$   ii. A golyó pályája megfordítható, így az eredeti kérdés helyett vizsgálhatjuk ezt is: legalább mekkora sebességgel kell az épület tetejéről eldobni a golyót, hogy valahol földet érjen (anélkül, hogy az épületnek ütközne). Könnyen belátható, hogy a golyó pályája vagy az 1. ábrán látható, az épületet érintő parabola, vagy pedig egy olyan vízszintes hajítás, ahol a parabola görbülete a csúcspontjában megegyezik a gömb sugarával. (Ha a golyó sehol nem érinti a parabolát, akkor csökkenthető a sebessége, egész addig, amíg valahol érinteni fogja.) 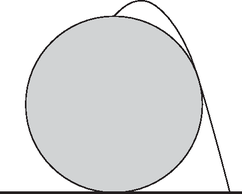  1. ábra   Vizsgáljuk meg a vízszintes hajítást! Ha változatlan sebességgel, de a vízszinteshez képest kis szöggel felfelé dobnánk a golyót, akkor sehol sem érintené az épületet ‐ így viszont kezdeti sebessége csökkenthető lenne! Ebből következik, hogy a vízszintes hajítás nem lehet ideális, így a helyes megoldás az 1. ábrán látható pálya.   iii. Vegyük észre, hogy az egész épületnek benne kell lenni abban a tartományban, amit az épület tetejéről induló, minimális sebességű hajításokkal el tudnánk találni. (Hiszen ha az optimálishoz képest csökkentjük az eldobás vízszintessel bezárt szögét, akkor a golyó nem érinti, hanem eltalálja az épületet.) Ugyanakkor a dobással elérhető tartomány határának érinteni kell az épületet. (Ellenkező esetben az optimális sebességgel lehetne úgy hajítani, hogy az nem érinti az épületet.) Tehát a minimális sebességgel eldobott golyóval elérhető tartomány határa és az épület felszíne érinti egymást (a szimmetria miatt két pontban). Ha a minimális indítási sebesség a gömb tetejéről $v_0$, akkor a következő egyenletrendszert kapjuk: $\begin{array}{c}{\displaystyle x^2+z^2+2zR=\mathrm{0,}z=\frac{v_0^2}{2g}-\frac{g{x}^2}{2v_0^2}\mathrm{.}}\end{array}$ $z$ kiküszöbölésével $x^2$-re a következő másodfokú egyenlet adódik: $\begin{array}{c}{\displaystyle {\left(\frac{g}{2v_0^2}\right)}^2{x}^4+\left(\frac{1}{2}-\frac{gR}{v_0^2}\right)x^2+\left(\frac{v_0^2}{4g}+R\right)\frac{v_0^2}{g}=0.}\end{array}$ A két görbe akkor érinti egymást, amikor az egyenlet diszkriminánsa éppen 0. Ebből $\begin{array}{c}{\displaystyle {\left(\frac{1}{2}-\frac{gR}{v_0^2}\right)}^2=\frac{1}{4}+\frac{gR}{v_0^2}\mathrm{,}\text{azaz}{v}_0^2=\frac{gR}{2}\mathrm{.}}\end{array}$ A mechanikai energia megmaradása alapján a keresett minimális indítási sebesség $\begin{array}{c}{\displaystyle v_{\underset{}{\overset{}{\text{min}}}}=\sqrt[]{v_0^2+4gR}=3\sqrt[]{\frac{gR}{2}}\mathrm{.}}\end{array}$   B rész. Légáramlás a szárny körül. i. A szárnyhoz rögzített vonatkoztatási rendszerben a kontinuitási törvény miatt két áramvonal között (egy áramlási vonal mentén) állandó a levegő térfogatárama (az időegységenként átáramló levegő mennyisége). A térfogatáram a sebesség és a keresztmetszet szorzata. A keresztmetszet viszont esetünkben ‐ a kétdimenziós geometria miatt ‐ arányos az áramvonalak távolságával, ami a 2. ábráról leolvasható. Mivel nincsen szél, a nyugalomban lévő levegő sebessége a szárnyhoz viszonyítva éppen $v_0$. Az ábrán megmérve $a=10$ egység és $b=13$ egység. Ez alapján a levegő sebessége a $P$ pontban a szárnyhoz képest $u=v_0\frac{a}{b}$, a földhöz képest pedig 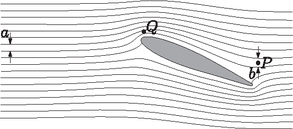$\begin{array}{c}{\displaystyle v_P=v_0-u=v_0\left(1-\frac{a}{b}\right)=23\frac{\text{m}}{\text{s}}\mathrm{.}}\end{array}$   2. ábra     ii. Bár az $\frac{1}{2}\rho v^2$ dinamikus nyomás aránylag kicsi, változása bizonyos mértékű adiabatikus összenyomódást vagy kitágulást eredményez. Ott, ahol a levegő kitágul, a hőmérséklete lecsökken, és ha a hőmérséklet eléri a harmatpontot, akkor a vízgőz kicsapódik, apró vízcseppek jelennek meg. A kicsapódás ott kezdődik meg, ahol a kitágulás maximális, azaz ahol a levegő (statikus) nyomása minimális. A Bernoulli-törvény szerint $p+\frac{1}{2}\varrho v^2=$ állandó, így $p$ ott lesz a legkisebb, ahol $v$ (a levegő szárnyhoz viszonyított sebessége) a legnagyobb, azaz ahol az áramvonalak a legközelebb vannak egymáshoz. Ez a 2. ábrán $Q$-val jelölt pont.   iii. Először meg kell határoznunk a harmatpontot. A vízgőz nyomása $p_{\text{w}}=p_{\text{sa}}r=\mathrm{2,08}\text{kPa}$. A kis változások miatt a gőznyomás hőmérséklet-függését tekinthetjük közelítőleg lineárisnak: $\begin{array}{c}{\displaystyle \frac{p_{\text{sa}}-p_{\text{w}}}{T_a-T}=\frac{p_{\text{sa}}-p_{sb}}{T_a-T_b}\mathrm{,}}\end{array}$ amiből $T\approx 291\mathrm{,}5\text{K}$ adódik. Ezután meg kell határozni a levegő sebessége és hőmérséklete közti kapcsolatot. A Bernoulli-törvényhez hasonlóan egy energiamérleget írhatunk fel, de figyelembe kell vennünk a levegő összenyomásával/kitágulásával kapcsolatos munkát is. Mivel a levegő rossz hővezető, és az áramlás során gyorsak a változások, a folyamat adiabatikus. Egy áramlási cső (például két közeli áramvonal közötti térrész) két pontjára (1 és 2) felírva a munkatételt egy mol levegőre az $\begin{array}{c}{\displaystyle \frac{1}{2}M{v}_1^2+c_{V}M{T}_1+p_1{V}_1=\frac{1}{2}M{v}_2^2+c_{V}M{T}_2+p_2{V}_2}\end{array}$ összefüggést kapjuk, ahol $M$ a levegő moláris tömege, $c_V$ pedig az állandó térfogaton mért fajhő. (Az első tag a gáz mozgási energiája, a második a belső energiája, a harmadik pedig a gáz benyomásakor végzett munka.) Felhasználva, hogy egy mol gázra $pV=RT$, és $c_{V}M+R=c_{p}M$, azt kapjuk, hogy $\frac{1}{2}{v}^2+c_{p}T=$ állandó. Ebből $\begin{array}{c}{\displaystyle c_p\Delta T=-\Delta \frac{v^2}{2}=\frac{1}{2}{v}_{\text{krit.}}^2\left(1-\frac{a^2}{c^2}\right)\mathrm{,}}\end{array}$ ahol $c$ az áramvonalak távolsága a $Q$ pontban. Felhasználva, hogy $c\approx 4\mathrm{,}5$ egység és $\Delta T=-1\mathrm{,}5\text{K}$, $\begin{array}{c}{\displaystyle v_{\text{krit.}}=c\sqrt[]{\frac{2c_p\Delta T}{c^2-a^2}}\approx 23\frac{\text{m}}{\text{s}}\mathrm{.}}\end{array}$   Megjegyzés: A valóságban ennél valamivel nagyobb sebesség szükséges, mert a levegő hirtelen kicsapódása csak jelentős túltelítés hatására indul meg.   C rész. Mágneses csövek. i. A cső szupravezető falán nem mehetnek át indukcióvonalak, így a csőben állandó a fluxus. A cső belsejében örvénymentes a tér, a két feltételből együtt pedig adódik, hogy homogén is, azaz az indukcióvonalak párhuzamosak, és egyenlő távolságra vannak egymástól.   Megjegyzés: A csövön kívül a tér hasonlít a vékony, hosszú tekercs (szolenoid) mágneses teréhez, azzal a fontos különbséggel, hogy a szolinoid végeinek közelében a tekercs oldalán is lépnek ki indukcióvonalak, a szupravezető csőnél ez nem lehetséges. A másik különbség: a szolenoid árama (egyenletes tekercselés esetén) hosszegységenként mindenhol ugyanakkora, a szupravezető cső falában folyó áram pedig a végek közelében nem egyenletes.   A szupravezető cső indukcióvonalait vázlatosan a 3. ábra mutatja.   3. ábra     ii. Nyújtsuk meg gondolatban egy kicsiny $\Delta \ell$ értékkel a csövet, és vizsgáljuk meg, hogy ehhez mennyi munkára van szükség! A cső fluxusa nem változhat (mert a fluxusváltozás a szupravezetőben végtelen nagy áramokat indukálna), így a mágneses indukció is állandó: $B=\frac{\Phi }{\pi r^2}$. A mágneses tér energiasűrűsége $\frac{1}{2{\mu }_0}{B}^2$, amiből a cső megnyújtásához szükséges munka $\begin{array}{c}{\displaystyle \Delta W=\frac{1}{2{\mu }_0}{B}^2\Delta V=\frac{1}{2{\mu }_0}\frac{{\Phi }^2}{{\pi }^2{r}^4}\pi r^2\Delta \ell =\frac{{\Phi }^2}{2{\mu }_0\pi r^2}\Delta \ell \mathrm{.}}\end{array}$ Ezt a munkát a húzóerő végzi: $\Delta W=T\Delta \ell$, amiből a keresett erő $\begin{array}{c}{\displaystyle T=\frac{{\Phi }^2}{2{\mu }_0\pi r^2}\mathrm{.}}\end{array}$   iii. A csövek között fellépő erő iránya ‐ az elrendezés szimmetriája miatt ‐ nyilván merőleges a csövek tengelyére. Az erő nagyságát egy elektrosztatikus analógia alapján fogjuk meghatározni. Vizsgáljuk meg, hogyan változik a rendszer mágneses energiája, ha az egyik csövet egy kicsit elmozdítjuk, eltávolítjuk a másiktól! A csövek belsejében semmi se változik, mert a csövek fluxusa állandó, csak a külső tér változik. A csöveken kívül a mágneses indukció örvénymentes (mert nincsenek áramok), a csövek végpontjai $\pm \Phi$ erősségű források, ezeken kívül viszont mindenhol forrásmentes a tér. Ezek a csöveken kívül pontosan olyan feltételek, mint amilyenek négy $\pm Q$ nagyságú elektromos töltés elektromos terét jellemzik. (A csöveken belül természetesen különböző a két tér, és a csövek falai is az elektromos esettől különböző határfelületet jelentenek, de három dimenzióban a vékony csövek elhanyagolható módon torzítják a csöveken kívüli teret.) Ezek szerint a csövek végpontjait úgy tekinthetjük, mintha mágneses ponttöltések lennének. Keressük meg az elektromos és a mágneses jelenségek közötti megfeleltetést! Két $Q$ nagyságú, egymástól $a$ távolságra elhelyezett elektromos töltés között $F=\frac{1}{4\pi {\epsilon }_0}\frac{Q^2}{a^2}$ erő hat. Az egyik töltés terének energiasűrűsége a másik töltés helyén $\begin{array}{c}{\displaystyle w=\frac{{\epsilon }_0}{2}{E}^2=\frac{1}{32{\pi }^2{\epsilon }_0}\frac{Q^2}{a^4}\mathrm{.}}\end{array}$ Ezek szerint az erőt írhatjuk $F=8\pi w{a}^2$ alakban is. Ez a kifejezés bármely esetben használható két ellentétes előjelű, azonos nagyságú ponttöltés között fellépő erő meghatározására, így használhatjuk a mágneses ponttöltésekre is. A Gauss-törvény alapján egy $\Phi$ fluxusú mágneses ponttöltés által $a$ távolságra létrehozott indukció $B=\frac{\Phi }{4\pi a^2}$. Az energiasűrűség a ponttöltéstől $a$ távolságra $\begin{array}{c}{\displaystyle w=\frac{1}{2{\mu }_0}{B}^2=\frac{1}{32{\pi }^2{\mu }_0}\frac{{\Phi }^2}{a^4}\mathrm{,}}\end{array}$ amiből az $a$ távolságra lévő $\Phi$ fluxusú mágneses ponttöltések között fellépő erő $\begin{array}{c}{\displaystyle F=8\pi w{a}^2=\frac{1}{4\pi {\mu }_0}\frac{{\Phi }^2}{a^2}\mathrm{.}}\end{array}$ A négy ponttöltés közül az ellentétesek vonzzák egymást,   a köztük fellépő erő $F_1=\frac{1}{4\pi {\mu }_0}\frac{{\Phi }^2}{{\ell }^2}$. Az átlósan elhelyezkedő azonos előjelű töltések közti taszítóerő normális komponense $\begin{array}{c}{\displaystyle F_2=\frac{\sqrt[]{2}}{2}\frac{1}{4\pi {\mu }_0}\frac{{\Phi }^2}{2{\ell }^2}\mathrm{.}}\end{array}$ Az eredő vonzó erő ezek alapján $\begin{array}{c}{\displaystyle F=2\left(F_1-F_2\right)=\frac{4-\sqrt[]{2}}{8\pi {\mu }_0}\frac{{\Phi }^2}{{\ell }^2}\mathrm{.}}\end{array}$