Feladat:	2011. évi Nemzetközi Fizika Diákolimpia 1. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Honyek Gyula ,  Vankó Péter ,  Vigh Máté
Füzet:	2011/november, 489 - 490. oldal		PDF  |  MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia, Pontrendszerek mozgásegyenletei, Mesterséges holdak
Hivatkozás(ok):	Feladatok: 2011/október: 2011. évi Nemzetközi Fizika Diákolimpia 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 1. feladat. Egy háromtest-probléma és a LISA 1.1. A két tömegpont mozgásegyenlete: 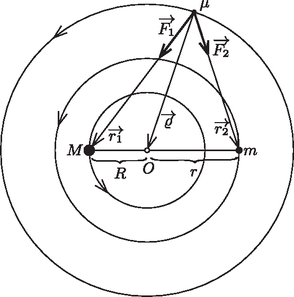${\displaystyle \begin{array}{cc}\hfill {\displaystyle m{\omega }_0^{2}r}& {\displaystyle =G\frac{mM}{{\left(r+R\right)}^2}\mathrm{,}}\hfill \\ \multicolumn{3}{c}{\text{<div style="line-height: 6pt"> </div>}}\\ \hfill {\displaystyle M{\omega }_0^{2}R}& {\displaystyle =G\frac{mM}{{\left(r+R\right)}^2}\mathrm{.}}\hfill \end{array}}$ Bármelyik egyenletet rendezve, és felhasználva, hogy $\begin{array}{c}{\displaystyle \frac{M}{r}=\frac{m}{R}=\frac{M+m}{R+r}\mathrm{,}}\end{array}$ a keresett szögsebesség $\begin{array}{c}{\displaystyle {\omega }_0=\sqrt[]{G\frac{M+m}{{\left(R+r\right)}^3}}\mathrm{.}}\end{array}$   1.2. A $\mu$ tömeg infinitezimálisan kicsi, ezért gravitációs ereje nem befolyásolja a másik két test mozgását.     1. ábra   A $\mu$ tömegű testet is a rá ható gravitációs erők eredője tartja körpályán (1. ábra): $\begin{array}{c}{\displaystyle \overrightarrow{F_1}+\overrightarrow{F_2}=\mu {\omega }_0^2\overrightarrow{\varrho }\mathrm{,}}\end{array}$ vagyis $\begin{array}{c}{\displaystyle G\frac{M\mu }{r_1^3}\overrightarrow{r_1}+G\frac{m\mu }{r_2^3}\overrightarrow{r_2}=G\mu \frac{M+m}{{\left(R+r\right)}^3}\overrightarrow{\varrho }\mathrm{.}}\end{array}$ Másrészt a tömegközéppont definíciója szerint $\begin{array}{c}{\displaystyle \overrightarrow{\varrho }=\frac{M\overrightarrow{r_1}+m\overrightarrow{r_2}}{M+m}\mathrm{,}}\end{array}$ amit behelyettesítve, és egyszerűsítve $\begin{array}{c}{\displaystyle \frac{M}{r_1^3}\overrightarrow{r_1}+\frac{m}{r_2^3}\overrightarrow{r_2}=\frac{M}{{\left(R+r\right)}^3}\overrightarrow{r_1}+\frac{m}{{\left(R+r\right)}^3}\overrightarrow{r_2}\mathrm{.}}\end{array}$ A fenti egyenlet két oldalán $\overrightarrow{r_1}$ és $\overrightarrow{r_2}$ együtthatói külön-külön meg kell egyezzenek, ahonnan $r_1=r_2=R+r$ adódik, vagyis a három test egy szabályos háromszög csúcsain helyezkedik el. A koszinusztétel alapján $\begin{array}{c}{\displaystyle {\varrho }^2=R^2+r^2-2R\left(R+r\right)\text{cos}{60}^{\circ }=R^2+Rr+r^2\mathrm{.}}\end{array}$ Ezek szerint 1.2.1. $\mu$ és $M$ távolsága: $r_1=R+r$, 1.2.2. $\mu$ és $m$ távolsága: $r_2=R+r$, 1.2.3. $\mu$ és a tömegközéppont távolsága: $\varrho =\sqrt[]{R^2+Rr+r^2}$.   1.3. A feladat az egyensúlyi helyzet körüli kis rezgések körfrekvenciájának meghatározása volt. Ehhez a versenyzők azt az útmutatást kapták, hogy tételezzék fel a rezgő test perdületének megmaradását. Ebből kiindulva és még az energia megmaradását is felírva hosszas számolás után az $\omega =\sqrt[]{7}{\omega }_0/2$ eredmény kapható (lásd a http://www.ipho2011.org/contents/problems_solutions honlapon a ,,hivatalos'' megoldást). Sajnos ez a megoldás hibás! A korlátozott háromtest-problémában (amikor az egyik test tömege elhanyagolhatóan kicsi a másik kettőé mellett) sem a kis test perdülete, sem a mechanikai energiája nem megmaradó mennyiség! Ténylegesen még a vizsgált pont stabilitása sem valósul meg, ha $m/M>0\mathrm{,}04$; márpedig a feladatban a $m=M$ speciális esetet kellett volna vizsgálni. Ekkor a kérdéses pont (a szabályos háromszög egyik csúcspontja) körül egyáltalán nem alakulhatnak ki harmonikus rezgések!   1.4. Az űrhajók egymás körül is $\omega$ szögsebességgel keringenek, így a relatív sebességük $\begin{array}{c}{\displaystyle v_{\text{rel.}}=L\omega =\frac{2\pi }{T}L\mathrm{,}}\end{array}$ ahol $L$ a ,,karok'' hossza, $T$ pedig a Föld keringési ideje. Behelyettesítve $\begin{array}{c}{\displaystyle v_{\text{rel.}}=996\frac{\text{m}}{\text{s}}\mathrm{.}}\end{array}$