Feladat:	4468. fizika feladat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Szathmári Balázs
Füzet:	2013/február, 112 - 113. oldal		PDF  |  MathML
Témakör(ök):	Feladat, Súlypont (tömegközéppont) meghatározása
Hivatkozás(ok):	Feladatok: 2012/október: 4468. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.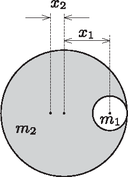   Megoldás. Ha a lemez vastagsága $d$, anyagának sűrűsége pedig $\varrho$, akkor a nagy körlap tömege $\begin{array}{c}{\displaystyle m_0=R^2\pi \varrho d\mathrm{,}}\end{array}$ a kivágott kis körlap tömege $\begin{array}{c}{\displaystyle m_1=r^2\pi \varrho d\mathrm{,}}\end{array}$ és a maradék darab tömege $\begin{array}{c}{\displaystyle m_2=m_0-m_1=\left(R^2-r^2\right)\pi \varrho d\mathrm{.}}\end{array}$     1. ábra   A kivágott kis körlap tömegközéppontja a körlemez középpontjától mérve $x_1=R-r$ távolra esik. A ,,lyukas körlap'' tömegközéppontja valamekkora $x_2$ távolságra kerül a körlemez középpontjától, és a feladat szövege szerint $x_2\le \frac{R}{100}$ (1. ábra). A nagy körlap a kis körlapból és a lyukas körlapból áll össze, így a nagy körlap tömegközéppontja (ami nyilván a geometriai középpontjába esik) a két összetevő tömegközéppontjainak koordinátáiból és a tömegeikből számítható: $\begin{array}{c}{\displaystyle x_0=\frac{m_1{x}_1-m_2{x}_2}{m_1+m_2}=0.}\end{array}$ Innen $\begin{array}{c}{\displaystyle x_2=\frac{m_1}{m_2}{x}_1=\frac{r^2}{R^2-r^2}\left(R-r\right)=\frac{r^2}{R+r}\le \frac{R}{100}\mathrm{.}}\end{array}$ Legyen a kérdéses $r/R$ arány $a$, vagyis $r=aR$. (Nyilván $0<a<1$.) Ezzel a jelöléssel a fenti egyenlőtlenség: $\begin{array}{c}{\displaystyle \frac{a^2{R}^2}{aR+R}\le \frac{R}{100}\mathrm{,}\text{vagyis}100a^2\le a+1.}\end{array}$ Határesetben (amikor $x_2=R/100)$ egy másodfokú egyenletet kell megoldanunk, amelynek pozitív gyöke: $\begin{array}{c}{\displaystyle a_0=\frac{1+\sqrt[]{401}}{200}\approx 0\mathrm{,}105.}\end{array}$ Ha a $r/R$ arány nem nagyobb ennél az értéknél, akkor a lyukas körlemez tömegközéppontja legfeljebb $R/100$ távolságra lehet a tömör körlemez középpontjától.   Megjegyzés. A feladat általánosabban, $x_2=kR$ tömegközéppont-eltolódásra is megoldható. A sugarak $a=r/R$ aránya ilyenkor $\begin{array}{c}{\displaystyle a=\frac{k}{2}+\sqrt[]{{\left(\frac{k}{2}\right)}^2+k}\mathrm{,}}\end{array}$ illetve a fordított összefüggés: $\begin{array}{c}{\displaystyle k=\frac{a^2}{a+1}\mathrm{.}}\end{array}$   2. ábra   Ha $k\ll 1$, akkor $k\approx a^2$, vagyis a tömegközéppont (relatív) eltolódása a kivágott rész (relatív) területével egyezik meg. Érdekes a másik határeset is: ha $a\approx 1$ (vagyis ha szinte az egész körlemezt eltávolítjuk), akkor a maradék ,,vonalszerű'' alakzat tömegközéppontját $k=1/2$, vagyis $x_2=R/2$ jellemzi (2. ábra).